SBNet: Sparse Blocks Network for Fast Inference
Abstract
Conventional deep convolutional neural networks (CNNs) apply convolution operators uniformly in space across all feature maps for hundreds of layers - this incurs a high computational cost for real-time applications. For many problems such as object detection and semantic segmentation, we are able to obtain a low-cost computation mask, either from a priori problem knowledge, or from a low-resolution segmentation network. We show that such computation masks can be used to reduce computation in the high-resolution main network. Variants of sparse activation CNNs have previously been explored on small-scale tasks and showed no degradation in terms of object classification accuracy, but often measured gains in terms of theoretical FLOPs without realizing a practical speed-up when compared to highly optimized dense convolution implementations. In this work, we leverage the sparsity structure of computation masks and propose a novel tiling-based sparse convolution algorithm. We verified the effectiveness of our sparse CNN on LiDAR-based 3D object detection, and we report significant wall-clock speed-ups compared to dense convolution without noticeable loss of accuracy. ††Code available at https://github.com/uber/sbnet
1 Introduction
Deep convolutional neural networks (CNNs) have led to major breakthroughs in many computer vision tasks [21]. While model accuracy consistently improves with the number of layers [11], as current standard networks use over a hundred convolution layers, the amount of computation involved in deep CNNs can be prohibitively expensive for real-time applications such as autonomous driving.
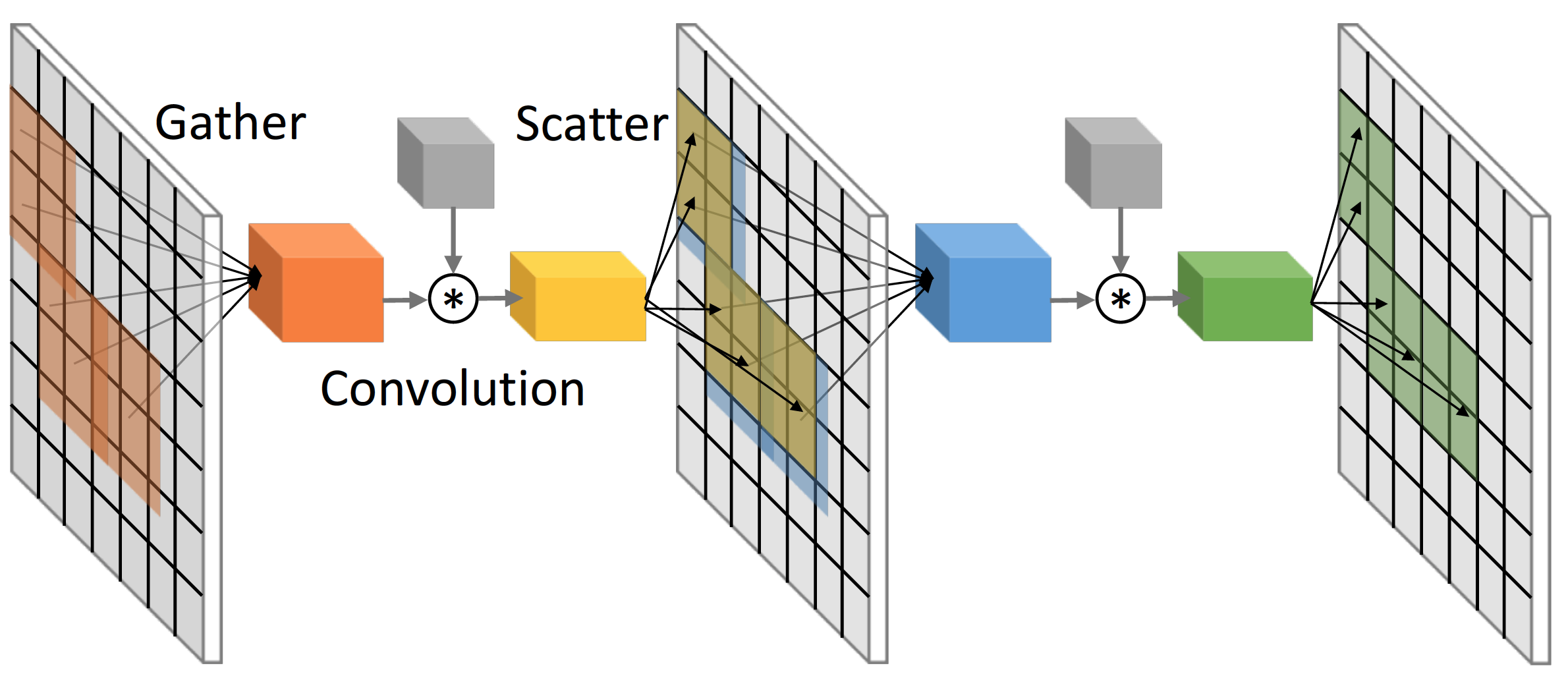
Spending equal amount of computation at all spatial locations is a tremendous waste, since spatial sparsity is ubiquitous in many applications: in autonomous driving, only the areas on the road matter for object detection; in video segmentation, only occluded and fast-moving pixels require recomputation; in 3D object classification [34], sparsity is directly encoded in the inputs as voxel occupancy. In these examples, spatial sparsity can be represented as binary computation masks where ones indicate active locations that need more computation and zeros inactive. In cases where such masks are not directly available from the inputs, we can predict them in the form of visual saliency [16] or objectness prior [20] by using another relatively cheap network or even a part of the main network itself [4, 25].
These binary computation masks can be efficiently incorporated into the computation of deep CNNs: instead of convolving the input features at every location, we propose to use the masks to guide the convolutional filters. Computation masks can also be considered as a form of attention mechanism where the attention weights are binary. While most current uses of attention in computer vision have been predominantly targeted at better model interpretability and higher prediction accuracy, our work highlights the benefit of attentional inference speed-up.
In this work, we leverage structured sparsity patterns of computation masks and propose Sparse Blocks Networks (SBNet), which computes convolution on a blockwise decomposition of the mask. We implemented our proposed sparse convolution kernels (fragments of parallel code) on graphics processing unit (GPU) and we report wall-clock time speed-up compared against state-of-the-art GPU dense convolution implementations. Our algorithm works well with the popular residual network (ResNet) architectures [11] and produces further speed-up when integrated within a residual unit.
Our sparse block unit can serve as a computational module in almost all deep CNNs for various applications involving sparse regions of interest, bringing inference speed-up without sacrificing input resolution or model capacity. We evaluate the effectiveness of our SBNet on LiDAR 3D object detection tasks under a top-down bird’s eye view, and we leverage both static road maps and dynamic attention maps as our computation masks. We found SBNet achieves significant inference speedup without noticeable loss of accuracy.
2 Related work
Sparse computation in deep learning has been extensively explored in the weights domain, where the model size can be significantly reduced through pruning and low-rank decomposition [17, 27, 10, 32, 24, 14]. However it is not trivial to achieve huge speed-up from sparse filters without loss of accuracy because a single filter channel is rarely very close to zero at every point. [24, 12] explored structured sparsity by pruning an entire filter. Other forms of redundancies can also be leveraged such as weight quantization [39, 2], teacher-student knowledge distillation [13], etc.
On the other end, in the activation domain, sparsity was also explored in various forms. Rectified linear unit (ReLU) activations contain more than 50% zero’s on average and speed-up can be realized on both hardware [19] and algorithmic level [30]. Activation sparsity can also be produced from a sparse multiplicative gating module [3]. In applications such as 3D object classification, prior work also exploits structures in the sparse input patterns. OctNet [29] introduces novel sparse high-resolution 3D representation for 3D object recognition. Different from [29], [9] proposes a generic valid sparse convolution operator where the input density mask is applied everywhere in the network. As we will discuss later, while [9] implements a generic convolution operator, it is not suitable for moderately large input sizes.
When the inputs contain no structured sparsity, one can obtain dynamic computation masks during the inference process over hundreds of layers. [4] learns to skip an adaptive number of layers in ResNet for unimportant regions in object classification tasks. Similarly, [25] infers a pixel-wise mask for reweighting the computation in the context of semantic segmentation. [20] predicts objectness prior heat maps during network inference for more accurate object detection, but the heat maps do not help speed-up the inference process; instead, the authors resort to downsampled inputs for faster inference. Given the vast availability of those computation masks and heat maps during inference, our proposed sparse convolution operators can be jointly applied to achieve major speedup gains on full resolution.
Sparse inference is beneficial to accuracy as the network focuses more of its computational attention on useful activation patterns and ignores more of the background noise. For instance, sparse batch normalization (BN) [15, 31] is invariant to input sparsity level and outperforms regular BN in optical flow tasks. Here, we exploit the benefit of sparse BN within our sparse residual units. Sparse convolution can also help increase the receptive field and achieve better classification accuracy through perforated operations [5].
Sparse computation masks are also related to the attention mechanism. Prior work applied visual attention on convolutional features and obtained better model interpretability and accuracy on tasks such as image captioning [35], visual question answering [36, 28], etc. However, unlike human attention which helps us reason visual scenes faster, these attentional network structures do not speed up the inference process since the attention weights are dense across the receptive field. Instead, we consider the simple case where the attention weights are binary and explore the speed-up aspect of the attention mechanism in deep neural networks.
Comparison with im2col based sparse convolution algorithms
Here we discuss the main differences of our approach compared to popular sparse convolution algorithms based on matrix lowering, as seen in [27, 30, 3]. These methods all use the same type of matrix lowering which we refer as im2col. Widely known in the implementation of dense convolution in Caffe [18], im2col gathers sliding windows of shape , where is the filter window size and is the input channel count. active windows are then reshaped into rows of a matrix of shape multiplied with a lowered filter matrix with shape , where is the number of filters. This method is often faster than sparse matrix-vector product due to contiguous memory access and better parallelism. However, these methods introduce memory overhead and cannot leverage the benefits of Winograd convolution [33, 22]. Further, writing out the intermediate lowered results introduces additional memory bandwidth overhead. [9] designed a look-up table based data structure for storing sparsity, but it is still slower compared to highly optimized Winograd convolution. Our approach differs from [9, 25, 30] in that we gather block-wise slices from tensors and maintain the tensor shape instead of lowering them to vectors. Within each active block, we perform a regular dense convolution and build on top of a speedup from using Winograd convolution [33, 22] compared to general matrix-matrix multiplication (GEMM).
3 SBNet: Sparse Blocks Network
In this paper, we show that block sparsity can be exploited to significantly reduce the computational complexity of convolutional layers in deep neural networks. Unlike previous work taking advantage of unstructured sparsity, we show that our approach results in both theoretical and practical speed-up without loss of accuracy. We observe that many input sources have structured sparsity that meshes well with block sparsity - background pixels are likely to be surrounded by other background pixels. It stands to reason that computations for entire spatial clumps or “blocks” of activations can be skipped.
Block sparsity is defined in terms of a mask that can be known upfront from the input data domain knowledge and a priori sparsity structure, or can be computed using lower cost operations. In particular, we show the usefulness of our convolution algorithm on LiDAR object detection and we exploit the sparsity from the road and sidewalk map mask as well as the model predicted foreground mask at lower-resolution. For speed-up purposes, the same sparsity mask is reused for every layer in our experiments, but it can also be computed from a different source per layer. In particular, at different spatial scales within the network, we also use reduced spatial block sizes to better match the granularity of spatial activations at that scale.
The input to our sparse convolution module is a dense binary mask. Just like other standard sparse operations, we first need to extract a list of active location indices, which is named the reduce mask operation. Then, we would like to extract data from the sparse inputs at specified locations and paste the computed results back to the original tensor. To summarize, there are two major building blocks in our approach to sparse block-wise convolution:
-
Reduce mask to indices: converts a binary mask to a list of indices, where each index references the location of the corresponding -dimensional block in the input tensor and in our current implementation this is a 3- tuple (batch , -location, -location) shared across the channel dimension (see Figure 2).
-
Sparse gather/scatter: For gathering, we extract a block from the input tensor, given the start location and the size of the -d block. Scatter is the inverse operation where we update the output tensor using previously gathered and transformed data.
In this section, we first go over details of the above two building blocks, and then we introduce a sparse blocks residual unit which groups several layers of computation into sparse blocks. Then follows implementation details that are crucial to achieving a practical speed-up.
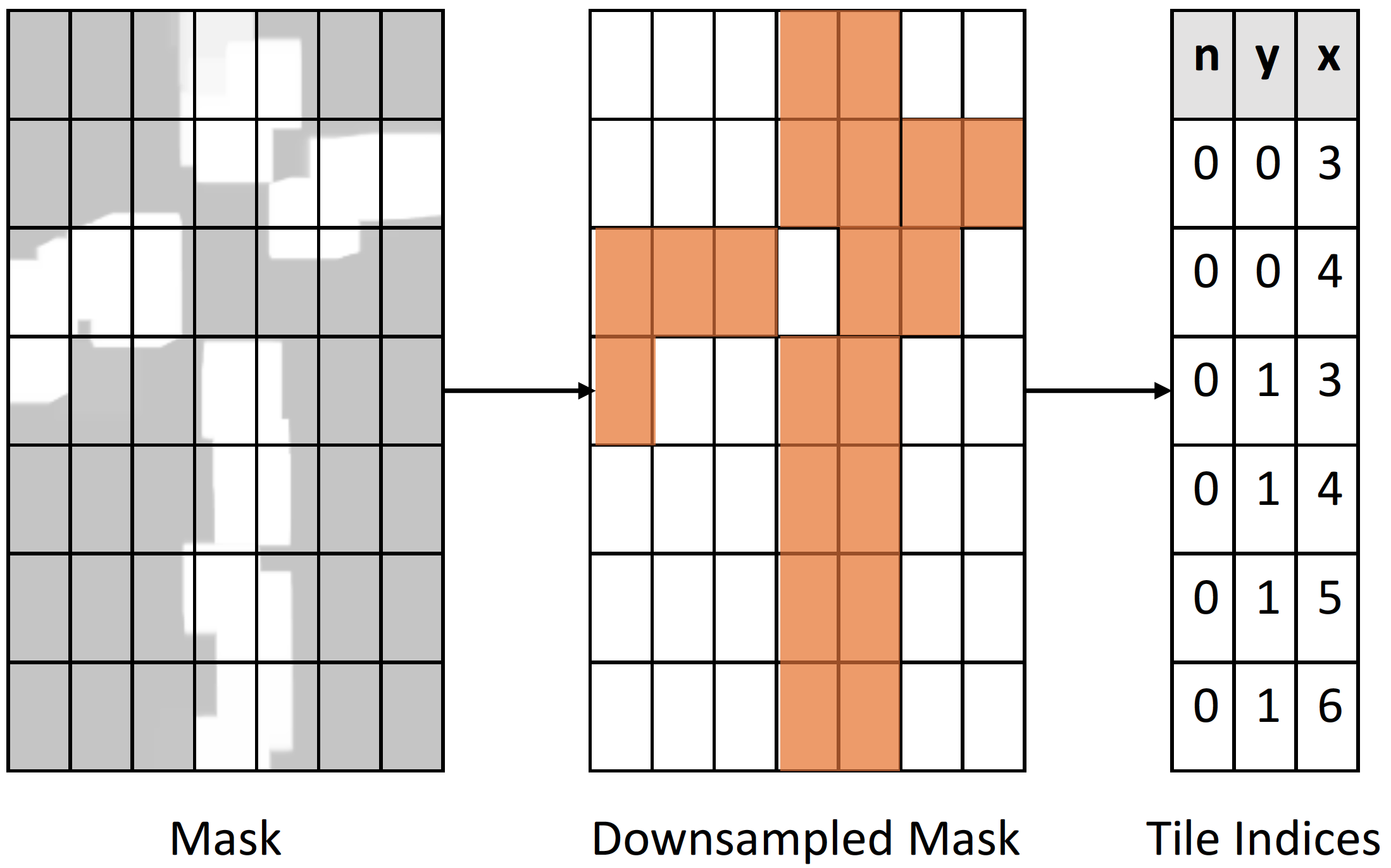
3.1 Reduce mask to indices
We start with a feature map of size . We will demonstrate this for the case of 2D convolutions but our approach is applicable to higher dimensions. Let be the binary mask representing the sparsity pattern. We would like to take advantage of non-sparse convolution operations as they have been heavily optimized. With this in mind, we propose to cover the non-zero locations with a set of rectangles. Unfortunately, covering any binary shape with a minimal number of rectangles is an NP-complete problem [6]. Furthermore, using rectangles of different shapes is hard to balance the computational load of parallel processors. Therefore, we chose to have a uniform block size, so that the gathered blocks can be batched together and passed into a single dense convolution operation.
In signal processing “overlap-add” and “overlap-save” are two standard partitioning schemes for performing convolutions with very long input signals [7]. Our sparse tiling algorithm is an instantiation of the “overlap-save” algorithm where we gather overlapping blocks, but during the scatter stage, each thread writes to non-overlapping blocks so that the writes do not require atomic locking. Knowing the block sizes and overlap sizes, we can perform a simple pooling operation, such as maximum or average pooling followed by a threshold to downsample the input mask. The resulting non-zero locations are the spatial block locations that we extract the patches from. Figure 3 illustrates our tiling algorithm.
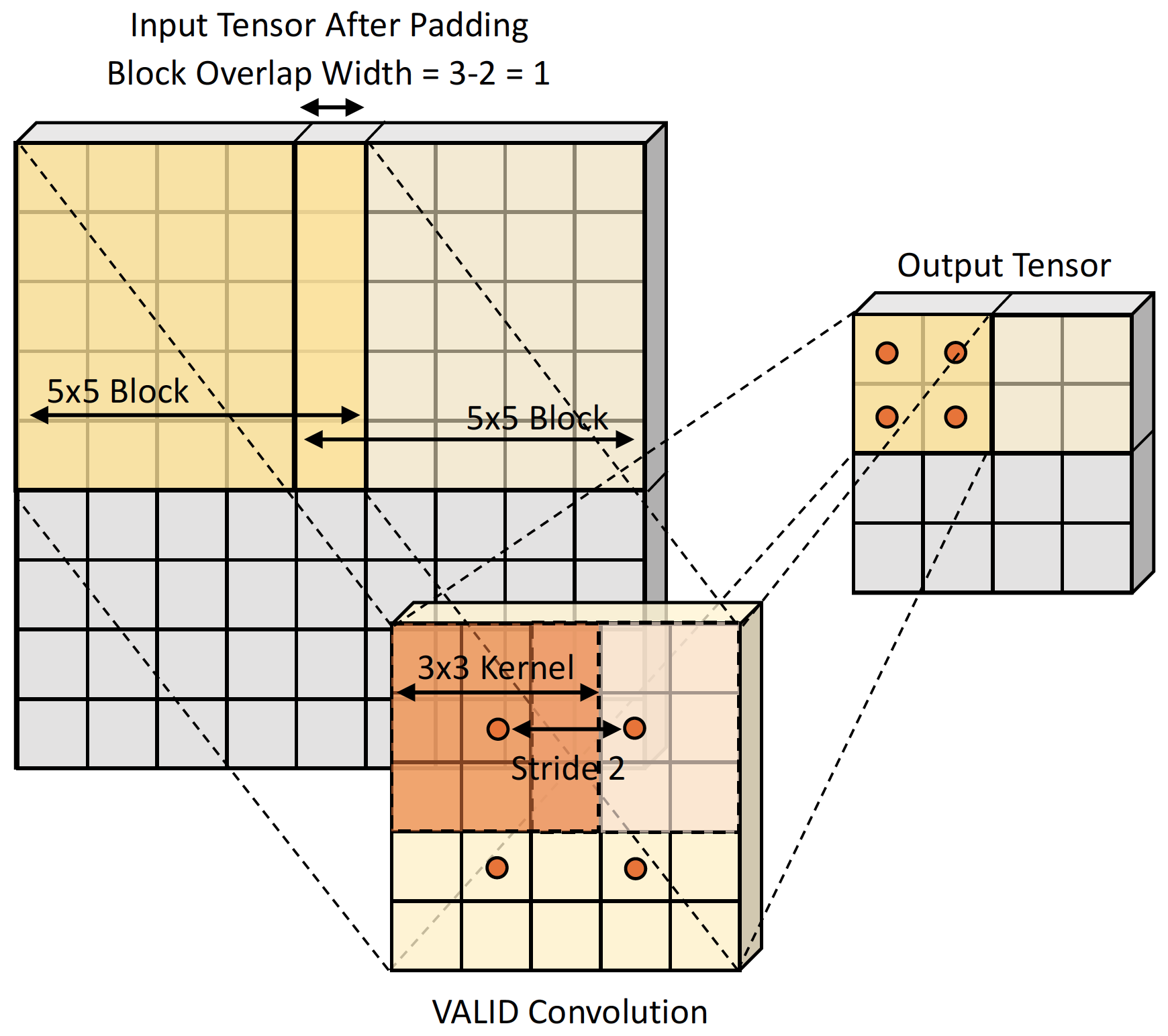
3.2 Sparse gather/scatter
Sparse gather/scatter operations convert the network between dense and sparse modes. Unlike regular gather/scatter kernels that are implemented in deep learning libraries (e.g. tf.gather_nd, tf.scatter_nd), our proposed kernels not only operate on dense indices but also expands spatially to their neighborhood windows. Patch extracting operations (e.g. tf.space_to_batch, tf.batch_to_space) also share some similarities with our approach but lack spatial overlap and indexing capability. This input overlap is essential to producing the output that seamlessly stitches the results of adjacent block convolutions in a way that is locally-equivalent to a dense convolution on a larger block. Here, we introduce the technical details of our proposed gather and scatter operations.
Gather kernel
Given a list of indices of size , where is the number of blocks, each has a tuple of (, , ) referencing the center location of the non-sparse blocks, we then slice the blocks out of the 4- input tensor using slices, where and are the blocks’ height and width, and stack the slices into a new tensor along the batch dimension, yielding a tensor.
Scatter kernel
Scatter is an operation inverse to gather, reusing the same input mask and block index list. The input to scatter kernel is a tensor of shape . For a mini-network shown in Figure 1, and are computed according to the output size reduction following a single unpadded convolution (also known as valid convolution). This convolution is slotted between the scatter and gather operations. When this convolution has a kernel size of and strides , then, , and . Figure 3 illustrates a toy example how the output sizes are calculated.
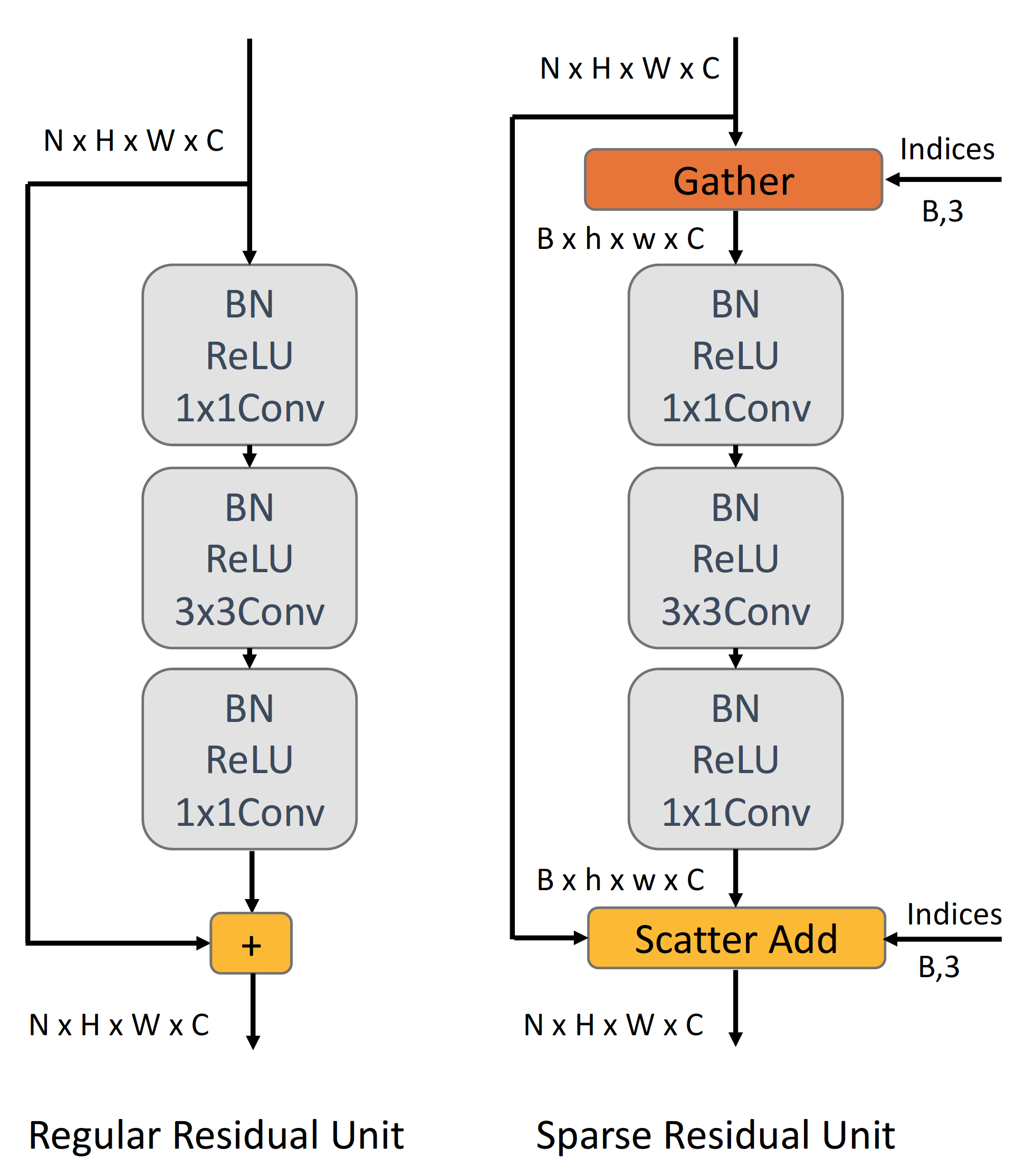
3.3 Sparse residual units
The ResNet architecture [11] is widely used in many state-of-the-art deep networks. Sparse residual units were previously explored using Valid Sparse Convolution proposed in [9]. Our proposed sparse blocks convolution also integrates well with residual units. A single residual unit contains three convolutions, batch normalization, and ReLU layers, all of which can be operated in sparse mode. The total increase in receptive field of a residual unit is the same as a single convolution. Therefore, all 9 layers can share a single pair of gathering and scattering operations without growing the overlap area between blocks. In addition to the computation savings, [31] showed that batch-normalizing across non-sparse elements contributes to better model accuracy since it ignores non-valid data that may introduce noise to the statistics. Figure 4 shows a computation graph of our sparse version of the residual unit.
End-to-end training of SBNet
is required since batch normalization (BN) statistics are different between full-scale activations and dense-only activations. The gradient of a scatter operation is simply the gather operation vice versa. When calculating the gradients of our overlapping gather operation, the scatter needs to perform atomic addition of gradients on the edges of overlapping tiles.
3.4 Implementation details
One of the major contributions of this work is an implementation of our block convolution algorithm using custom CUDA kernels. As we will show in our experiments, this results in a significant speed-up in terms of wall-clock time. This contrasts the literature, where only theoretical gains are reported [9]. In this section, we detail the techniques necessary to achieve such speed-ups in practice.
Fused downsample and indexing kernel
To minimize the intermediate outputs between kernels, we fused the downsample and indexing kernels into one. Inside each tile, we compute a fused max or average pooling operation followed by writing out the block index into a sequential index array using GPU atomics to increment the block counter. Thus the input is a tensor and the output is a list of sparse indices referring to full channel slices within each block.
Fused transpose+gather and transpose+scatter kernels
When performing 2D spatial gather and scatter, we favor format because of channel memory locality: in format, every memory strip of size is contiguous, whereas in format, only strips of size are contiguous. Because cuDNN library runs faster with data layout for convolutions and batch normalization, our gather/scatter kernel also fuses the transpose from to tensor data layout inside the same CUDA kernel. This saves a memory round-trip from doing additional transpose operations and is instrumental in achieving a practical speed-up.
Fused scatter-add kernel for residual blocks
For ResNet architecture during inference, the input tensor can be reused for output so that an extra memory allocation is avoided and there is no need to wipe the output tensor to be all zeros. We implemented a fused kernel of 2D scatter and addition, where we only update the non-sparse locations by adding the convolution results back to the input tensor.
4 Experiments
We validate our sparse blocks networks on our LiDAR 3D bird’s eye view (BEV) detection benchmark where the computation mask is available through offline road and sidewalk map information. In addition to using a static map-based mask, we also explored using dynamic attention masks with higher sparsity predicted by a small foreground segmentation network pretrained on dense box labels. We investigate two key aspects of our proposed model: 1) inference speed-up compared to a dense deep CNN detector; 2) change in detection accuracy brought by the use of sparse convolution.
Experiment environments
For all of the experiments, we implemented and benchmarked in TensorFlow 1.2.1 using cuDNN 6.0. Because TensorFlow by default uses tensor format it incurs a lot of overhead compared to cuDNN’s preferred format, we also implemented standard ResNet blocks in for a fair comparison. To compare with the sub-manifold sparse convolution [9], we benchmark using their released PyTorch implementation, using the same version of the cuDNN library. We use NVIDIA GTX 1080Ti for the layerwise benchmark, and NVIDIA Titan XP for the full network benchmark.
Choosing the optimal block sizes
Smaller block sizes produce higher mask matching granularity at the expense of increased boundary overlap. Larger blocks have a lower percentage of overlap, but depending on the feature map resolution, they are less usable due to their relative size to the total size of the feature map. To achieve the maximum speed-up we perform a search sweep over a range of block sizes to automatically pick the fastest-performing block decomposition.
4.1 Datasets
We used the following datasets for evaluating our LiDAR BEV detectors.
Tor4d
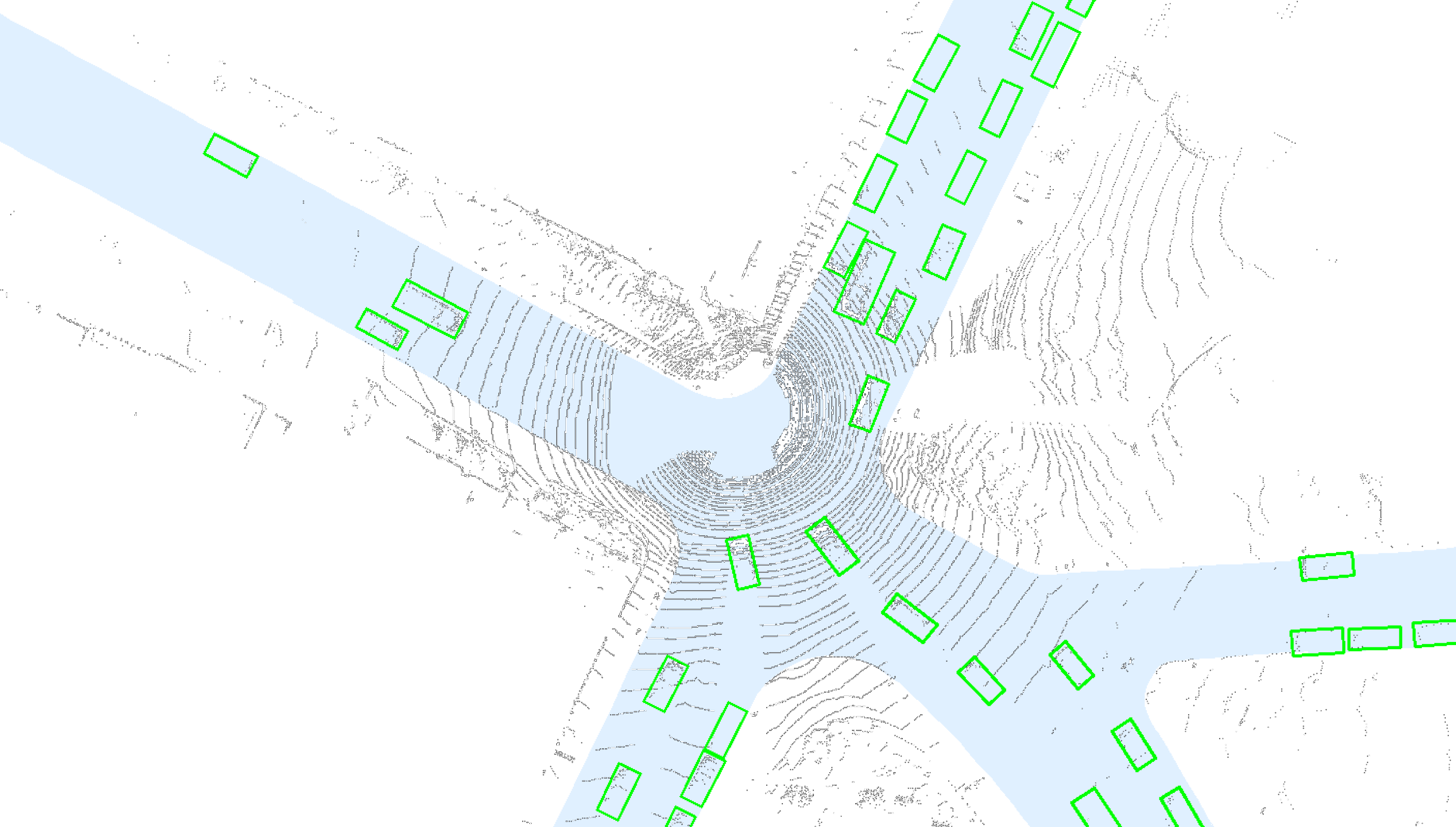
Our internal TOR4D LiDAR detection dataset consists of 1,239,437 training frames, 5,979 validation frames and 11,969 test frames. It also contains offline road map information, which can be directly served as the computation mask without additional processing. Each frame contains LiDAR point cloud sparse data for a region of 80m140.8m, with height ranging from -2m to 4m. We use discretization bin size 0.1m0.1m0.2m. Two extra bins on the -dimension are designated to points outside the height range limits and one additional channel is used to encode the LiDAR intensity. The input tensor of the detector is of size 800140833. Each frame has a corresponding crop of the road map, which is a top-down binary mask indicating which pixels belong to the road (see Figure 5).
Kitti
To compare with other published methods, we also run experiments on the KITTI 2017 BEV benchmark [8]. The dataset consists of 7,481 training frames and 7,518 test frames. Each frame contains a region of 80m70.4m, with height ranging from -3 to 1 m. We use discretization bin size 0.1m0.1m0.2m. Two extra bins on the -dimension are designated to points outside the height range limits and one additional channel is used to encode the LiDAR intensity. The input tensor of the detector is of size 80070423.
4.2 Model
3D object detector network
We adopt a fully convolutional detector architecture that resembles [26]. Our model has a residual network backbone and one convolutional and two upsampling layers with skip connections. For the residual backbone part, it has 2 initial convolution layers (conv-1), followed by [3, 6, 6, 3] residual units per residual block (conv-2 - conv-5), with channel depth [96, 192, 256, 384], and 16 downsampled activation size at the top of the backbone network. Two extra upsampling (deconvolution) layers are appended to bring the outputs back to 4 downsampled size, with skip connections from the outputs of conv-4 and conv-3. Three branches of the outputs predict object classes, box sizes and orientations respectively. Our sparse residual blocks and sparse convolutions are applied on all layers.
Foreground mask network
To predict foreground computation masks, we adopt a Pyramid Scene Parsing Network (PSPNet) [38] on a ResNet-18 architecture [11] at 8 downsampled input resolution. The network has no bottleneck layers and has one initial convolution layer, followed by [2, 2, 2, 2] residual units per residual blocks, with channel depth [32, 64, 128, 256]. The network is trained to predict dilated dense box pixel labels.
4.3 Experimental design
We first run standalone layerwise speed-up tests, and we compare our approach with the theoretical speed-up, i.e. 1/(1-sparsity), and the released implementation of sub-manifold sparse CNN [9] (“Sub-M”). Using the same activation size of our detector network, we test the speed-up on three types of masks:
-
Synthetic masks generated using the top-left sub-region of input images to measure the practical upper bound on speed-up.
-
Road map masks obtained from our offline map data in TOR4D.
-
Predicted masks obtained from the outputs of PSPNet.
We compare detection accuracy with two baselines:
-
Dense: a dense network trained on all detection groundtruth.
-
Dense w/ Road Mask: a dense network trained on detection groundtruth within the road mask, i.e. treating regions outside the road as the ignore region.
Our SBNets use computation masks from road and sidewalk maps and predicted masks, trained end-to-end with the same number of training steps as the dense baselines. Detection accuracy is evaluated with on-road vehicles only.

| Stage | Size | Sub-M ([9]) | SBNet (Ours) |
|---|---|---|---|
| conv-2 | 40070424 | 0.40 | 3.39 |
| conv-3 | 20035248 | 0.75 | 2.47 |
| conv-4 | 10017664 | 0.28 | 1.34 |
| conv-5 | 508896 | 0.13 | 0.88 |
| Stage | #Units | Size | Sub-M ([9]) | SBNet (Ours) |
|---|---|---|---|---|
| conv-2 | 3 | 40070496 | 0.52 | 8.22 |
| conv-3 | 6 | 200352192 | 1.65 | 6.27 |
| conv-4 | 6 | 100176256 | 0.85 | 3.73 |
| conv-5 | 3 | 5088384 | 0.58 | 1.64 |
4.4 Results and Discussion
Inference speed-ups for single convolution layers and residual blocks are listed in Table 1, 2, 3, 4. For single convolutions, our method achieves over 2 speed-up for sparsity at 90% at large resolutions, whereas for residual units we obtain a significantly higher speed-up by grouping multiple convolutions, BNs and ReLUs into a single sparse block sharing the sparse gather-transpose and sparse scatter-transpose computation costs.
Notably, [9] is slower than dense convolution on most activation sizes and sparsity values, whereas our Sparse Blocks achieve much higher speed-up on large resolution sizes, highlighting the practical contributions of our algorithm as increasing number of real-time applications involve high-resolution inputs and outputs.
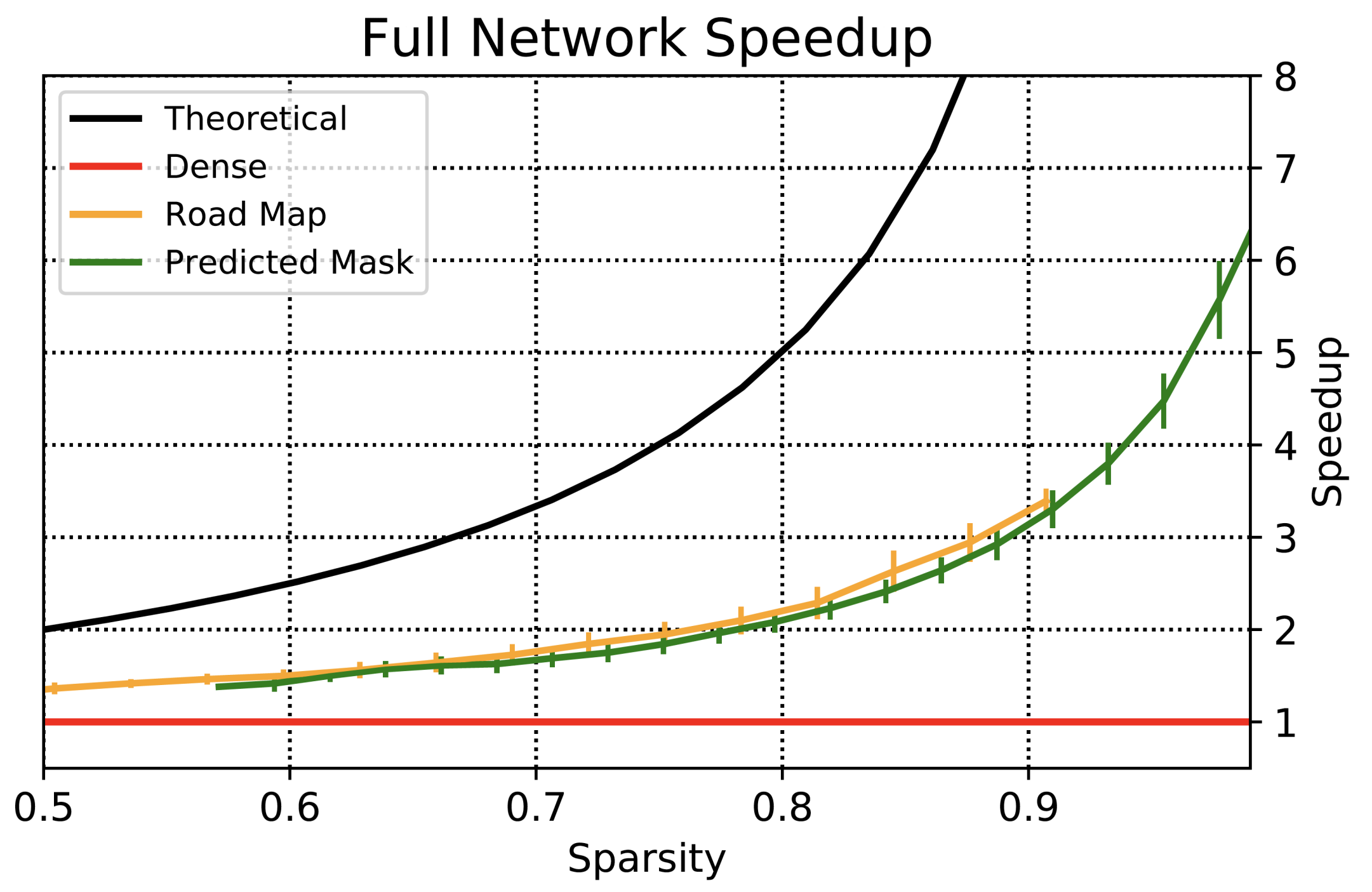
Figure 6 plots speed-up vs. sparsity on conv-2 residual blocks, for three types of different masks: synthetic, road map, and predicted. Road maps and predicted masks incur extra overhead compared to synthetic masks due to irregular shapes. Our method significantly closes the gap between real implementations and the theoretical maximum and does not slow down computation even at lower sparsity ratio such as 50 - 60%, which is the typically the least sparse road maps in our dataset. The computation masks output from the PSP network are 85 - 90% sparse on average, bringing up the speed-up for all sparse layers (Table 3), compared to using road masks (Table 4), which are only 70 - 80% sparse on average.
| Stage | #Units | Size | Sub-M ([9]) | SBNet (Ours) |
|---|---|---|---|---|
| conv-2 | 3 | 40070496 | 0.20 | 3.05 |
| conv-3 | 6 | 200352192 | 0.37 | 2.15 |
| conv-4 | 6 | 100176256 | 0.50 | 1.65 |
| conv-5 | 3 | 5088384 | 0.48 | 1.14 |
| Stage | #Units | Size | Sub-M ([9]) | SBNet (Ours) |
|---|---|---|---|---|
| conv-2 | 3 | 40070496 | 0.45 | 5.21 |
| conv-3 | 6 | 200352192 | 1.36 | 3.25 |
| conv-4 | 6 | 100176256 | 0.77 | 2.26 |
| conv-5 | 3 | 5088384 | 0.55 | 1.32 |
Table 5 reports detection accuracy on the TOR4D test set. We compare the road mask version of SBNet with a dense baseline that has training loss masked with the road mask for a fair comparison, since using road masks in the loss function hints learning more important regions. With a significant 1.8 speedup, SBNet contributes to another 0.3% gain in AP, suggesting that sparse convolution and normalization layers during inference can be beneficial dealing with sparse inputs. When using model predicted computation masks, we are able to reach 2.7 speedup, with detection accuracy slightly below our dense baseline.
Comparison of our approach and other published methods on KITTI can be found in Table 6. The dense detector baseline reached state-of-the-art performance in “Moderate” and “Hard” settings. The SBNet version of the detector achieves over 2.6 speed-up with almost no loss of accuracy. Including the cost of the mask network, our method is the fastest among the top performing methods on the KITTI benchmark, an order of magnitude faster than the published state-of-the-art [1].
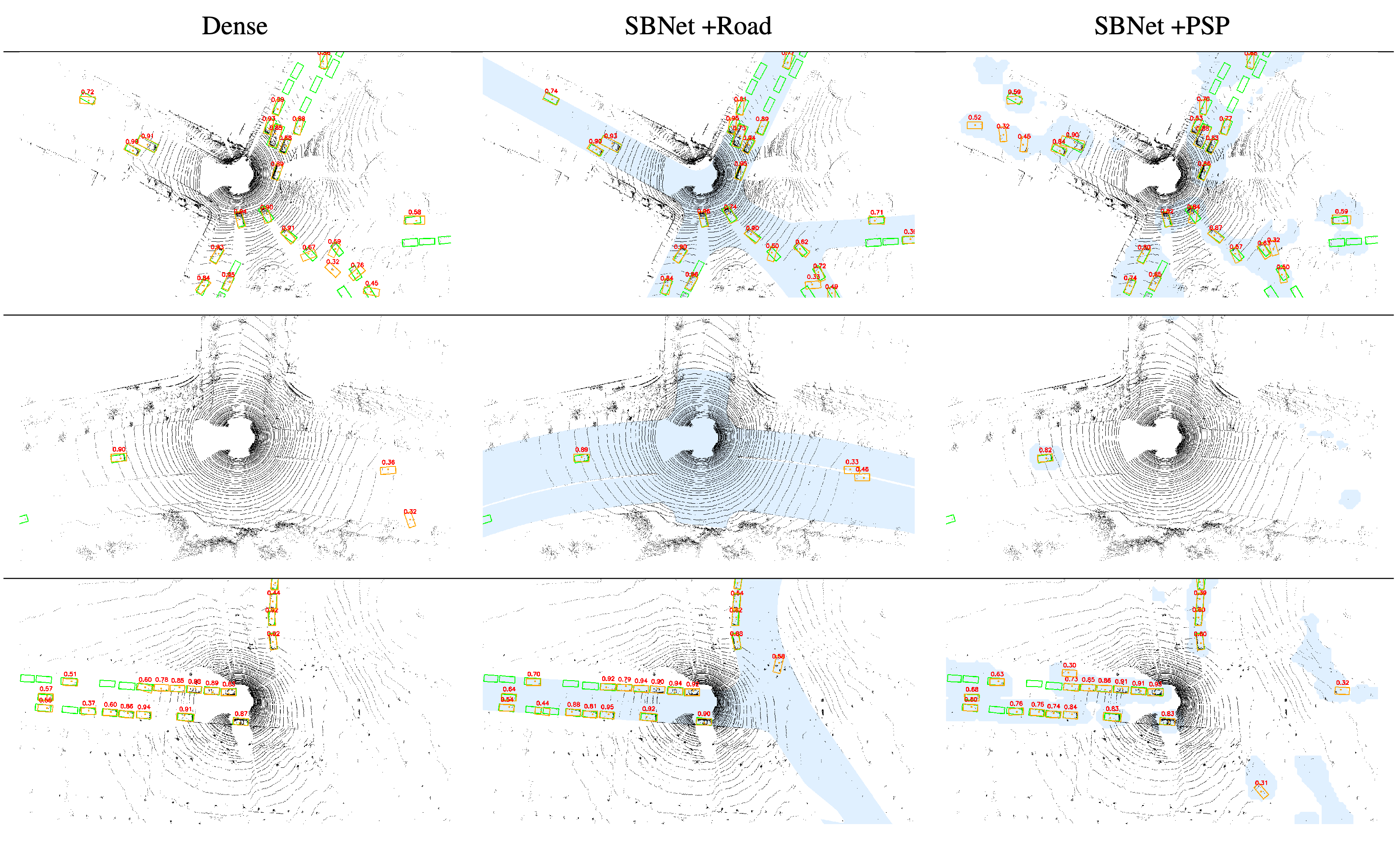
Detection results of our SBNet detector are visualized in Figure 8. As shown, PSPNet produces much sparser regions of interest compared to road maps while maintaining relatively competitive detection accuracy. Many false negative instances have too few LiDAR points and are difficult to be detected even by a dense detector.
Finally, we benchmark the computation overhead introduced by PSPNet in Table 7, which spends less than 4% of the time of a full dense pass of the detector network. SBNet and PSPNet combined together achieve 26.6% relative gain in speed compared to the Road Map counterpart. In addition to higher sparsity and speed-up, the predicted masks are much more flexible in areas without offline maps.
| Model | Train Loss | Sparsity | Avg. Speed-up | AP |
|---|---|---|---|---|
| Dense | Road Mask | 0% | 1.0 | 75.70 |
| SBNet +Road | Road Mask | 70% | 1.78 | 76.01 |
| Dense | No Mask | 0% | 1.0 | 73.28 |
| SBNet +PSP | PSP Mask | 86% | 2.66 | 73.01 |
| Model | Moderate | Easy | Hard | Avg. Time |
| DoBEM [37] | 36.95 | 36.49 | 38.10 | 600 ms |
| 3D FCN [23] | 62.54 | 69.94 | 55.94 | 5 s |
| MV3D [1] | 77.00 | 85.82 | 68.94 | 240 ms |
| Dense | 77.05 | 81.70 | 72.95 | 47.3 ms |
| SBNet | 76.79 | 81.90 | 71.40 | 17.9 ms |
| Network | Resolution | Time (ms) |
|---|---|---|
| Dense | 88.0 | |
| SBNet +Road | 49.5 | |
| SBNet +PSP | 33.1 | |
| PSPNet | 3.2 |
5 Conclusion and Future Work
In this work, we introduce the Sparse Blocks network which features fast convolution computation given a computation mask with structured sparsity. We verified significant wall-clock speed-ups compared to state-of-the-art dense convolution implementations. In LiDAR 3D detection experiments, we show both speed-up and improvement in detection accuracy using road map masks, and even higher speed-up using model predicted masks while trading off a small amount of accuracy. We expect our proposed algorithm to achieve further speed-up when used jointly with other orthogonal methods such as weights pruning, model quantization, etc. As future work, sparse blocks can be extended to a combination of different rectangle shapes (c.f. OctNet [29]) to get fine-grained mask representation, which can speed up inference with multi-scaled reasoning.
References
- [1] (2017) Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.4, Table 6.
- [2] (2017) Towards the limit of network quantization. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §2.
- [3] (2017) More is less: a more complicated network with less inference complexity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2, §2.
- [4] (2017) Spatially adaptive computation time for residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1, §2.
- [5] (2016) PerforatedCNNs: acceleration through elimination of redundant convolutions. In Advances in Neural Information Processing Systems (NIPS), Cited by: §2.
- [6] (1984) Optiml rectangle covers for convex rectilinear polygons. Ph.D. Thesis, Simon Fraser University. Cited by: §3.1.
- [7] (1994) Digital signal processing in communication systems. New York: Van Nostrand Reinhold. External Links: ISBN 0442016166 Cited by: §3.1.
- [8] (2012) Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.1.
- [9] (2017) Submanifold sparse convolutional networks. CoRR abs/1706.01307. External Links: Link Cited by: §2, §2, §3.3, §3.4, §4, §4.3, §4.4, Table 1, Table 2, Table 3, Table 4.
- [10] (2015) Learning both weights and connections for efficient neural networks. In Advances in Neural Information Processing Systems (NIPS), Cited by: §2.
- [11] (2016) Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1, §1, §3.3, §4.2.
- [12] (2017) Channel pruning for accelerating very deep neural networks. In Proceedings of the International Conference on Computer Vision (ICCV), Cited by: §2.
- [13] (2015) Distilling the knowledge in a neural network. CoRR abs/1503.02531. Cited by: §2.
- [14] (2017) Deep roots: improving cnn efficiency with hierarchical filter groups. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2.
- [15] (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Cited by: §2.
- [16] (1998) A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 20 (11), pp. 1254–1259. Cited by: §1.
- [17] (2014) Speeding up convolutional neural networks with low rank expansions. In Proceedings of the British Machine Vision Conference (BMVC), Cited by: §2.
- [18] (2014) Caffe: convolutional architecture for fast feature embedding. In Proceedings of the ACM International Conference on Multimedia, Cited by: §2.
- [19] (2017) Cnvlutin2: ineffectual-activation-and-weight-free deep neural network computing. CoRR abs/1705.00125. External Links: Link Cited by: §2.
- [20] (2017) RON: reverse connection with objectness prior networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1, §2.
- [21] (2012) ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems (NIPS), Cited by: §1.
- [22] (2016) Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2.
- [23] (2017) 3D fully convolutional network for vehicle detection in point cloud. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Cited by: Table 6.
- [24] (2017) Pruning filters for efficient convnets. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §2.
- [25] (2017) Not all pixels are equal: difficulty-aware semantic segmentation via deep layer cascade. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1, §2, §2.
- [26] (2017) Focal loss for dense object detection. In Proceedings of the International Conference on Computer Vision (ICCV), Cited by: §4.2.
- [27] (2015) Sparse convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2, §2.
- [28] (2016) Hierarchical question-image co-attention for visual question answering. In Advances in Neural Information Processing Systems (NIPS), Cited by: §2.
- [29] (2017) OctNet: learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2, §5.
- [30] (2017) Speeding up convolutional neural networks by exploiting the sparsity of rectifier units. CoRR abs/1704.07724. Cited by: §2, §2.
- [31] (2017) Sparsity invariant cnns. CoRR abs/1708.06500. Cited by: §2, §3.3.
- [32] (2016) Learning structured sparsity in deep neural networks. In Advances in Neural Information Processing Systems (NIPS), Cited by: §2.
- [33] (1980) Arithmetic complexity of computations. Vol. 33, SIAM. Cited by: §2.
- [34] (2015) 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1.
- [35] (2015) Show, attend and tell: neural image caption generation with visual attention. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Cited by: §2.
- [36] (2016) Stacked attention networks for image question answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §2.
- [37] (2017) Vehicle detection and localization on bird’s eye view elevation images using convolutional neural network. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Cited by: Table 6.
- [38] (2017) Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.2.
- [39] (2017) Incremental network quantization: towards lossless cnns with low-precision weights. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §2.