Probing Few-Shot Generalization with Attributes
Abstract
Despite impressive progress in deep learning, generalizing far beyond the training distribution is an important open challenge. In this work, we consider few-shot classification, and aim to shed light on what makes some novel classes easier to learn than others, and what types of learned representations generalize better. To this end, we define a new paradigm in terms of attributes—simple building blocks of which concepts are formed—as a means of quantifying the degree of relatedness of different concepts. Our empirical analysis reveals that supervised learning generalizes poorly to new attributes, but a combination of self-supervised pretraining with supervised finetuning leads to stronger generalization. The benefit of self-supervised pretraining and supervised finetuning is further investigated through controlled experiments using random splits of the attribute space, and we find that predictability of test attributes provides an informative estimate of a model’s generalization ability.
1 Introduction
While deep learning has led to numerous impressive success stories in recent years, generalizing far beyond the training distribution is a lingering challenge. Few-shot learning is a growing research area that aims at studying and improving upon a model’s ability to learn, for instance, new object classes, from only a few examples. However, traditional few-shot learning benchmarks are simplistic: while the test classes are disjoint from the training classes, they often represent visually and semantically similar concepts (Lake et al., 2011; Vinyals et al., 2016). Therefore it is difficult to measure whether performance on these benchmarks is indicative of generalization ability more broadly. Some recent benchmarks attempt to further separate train and test classes, by splitting at a higher semantic level when a class hierarchy is available (Ren et al., 2018) or holding out entire datasets Chen et al. (2019); Guo et al. (2020); Triantafillou et al. (2020), thus creating tougher generalization problems, but we are still lacking a comprehensive study of what underlies the ability to generalize better to some classes than to others.
In this work, we study this question through the lens of representation learning. We propose a new paradigm—few-shot attribute learning (FSAL)–for probing models’ few-shot generalization ability, based on attributes: simple building blocks that can be used to define class concepts, e.g., birds are warm-blooded vertebrates that lay eggs and have feathers. Humans also leverage similarity in the attribute space to recognize classes, which are “information-rich bundles of attributes that form natural discontinuities” (Rosch and Mervis, 1975). We use the relationship between attributes and classes to design a framework to measure generalization difficulty. Intuitively, if novel classes rely on attributes that were relevant for training classes, albeit perhaps different combinations of them, then it seems natural that those novel classes can be readily recognized with just a few labeled examples. But what if novel classes rely on attributes that are undefined or irrelevant during training? Will these classes be hard to learn?
Earlier empirical studies have examined the difficulty of few-shot learning based on other notions of similarity that, for instance, relies on the WordNet hierarchy Sariyildiz et al. (2021), or similarity of classes in the features space of pre-trained models Arnold and Sha (2021). Compared to these works, we directly leverage attributes to enable a more controlled study of tranferability and few-shot generalization. Empirically, we also explore both unsupervised and supervised approaches, revealing notably that a hybrid self-supervised and supervised approach achieves stronger generalization compared to other alternatives.
To summarize, our primary contributions are: 1) A new paradigm, FSAL, for studying generalization in few-shot learning; 2) Three new datasets serving as benchmarks for FSAL; 3) A study and analysis of different representation learning methods and their generalization capabilities in these tasks.
2 Few-Shot Attribute Learning
In this section, we define our few-shot attribute learning (FSAL) paradigm and highlight the additional challenges of FSAL compared to the standard few-shot learning of semantic classes.
Similar to standard few-shot learning (FSL), at test time, the learner is presented with an episode of data. The support set consists of positive and negative examples of the target attributes
| (1) |
where the or superscript suffix denotes whether the input is a positive or negative example. After rapid learning on the support set, the model is then evaluated on the binary classification performance of the query set:
| (2) |
As is standard in FSL, before the test episodes, we allow methods to learn a representation. In FSAL, this involves a labeled set of training attributes, but these must be disjoint from test attributes. For example, the model can learn attributes such as hair color and mustache during training, and will be tested on eyeglasses at test time. Similar to standard representation learning in FSL, training labels can be presented in the form of episodic labels for meta-learning methods, or absolute labels for pretraining-based methods. In FSAL, episodic labels refer to binary attribute labels in each episode, and absolute labels refer to attribute IDs.
At test time, the target binary label may concern a novel attribute that was previously unlabeled in the training set. For example, in one test episode, a smiling face with eyeglasses is positively labeled alongside other faces with eyeglasses. The task here is to learn the attribute of “wearing eyeglasses”. However, while the learner might have seen training images with eyeglasses, it was never a relevant feature for the purpose of predicting the positively labeled instances. For simplicity, each test episode is a binary classification problem. It can be easily extended to multiple new attributes by considering a few binary classification problems at the same time.
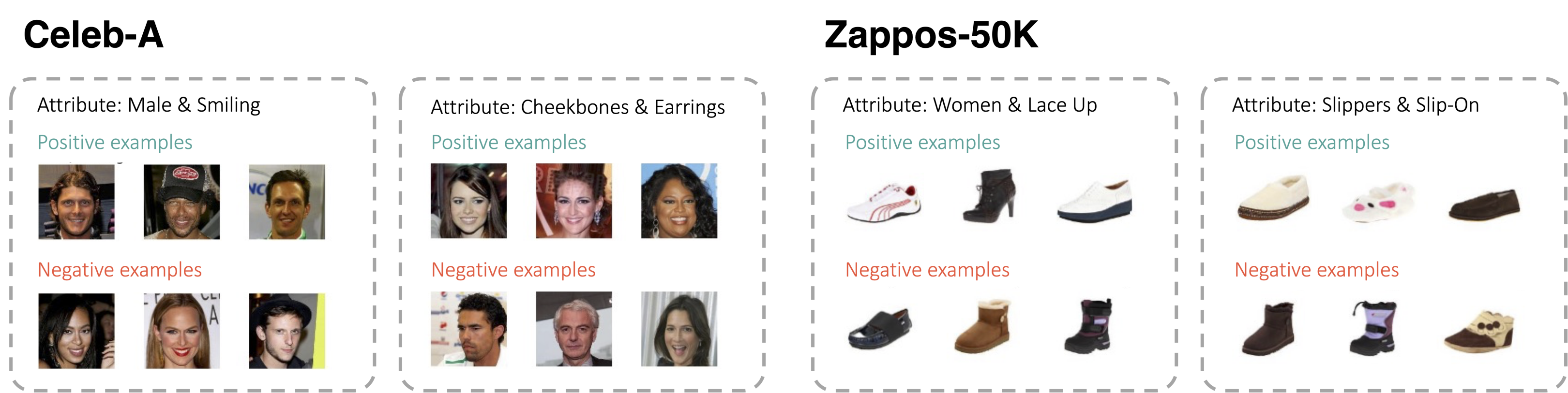
Furthermore, suppose that in another test episode, the same smiling face is positively labeled alongside other smiling faces. The target attribute here has now changed from “wearing eyeglasses” to “smiling.” This highlights a critical difference between few-shot attribute learning and standard few-shot learning of semantic classes: in standard FSL, each instance can belong to only one class regardless of the episode. In FSAL, due to the multi-label nature of the attribute space, one instance could have different labels depending on the context of the support set examples. Furthermore, there may be a large amount of ambiguity when the support set is small. Figure 1 shows a few examples of our attribute learning episodes. Note that in order to create task diversity, we allow both unary and binary attributes, where binary attributes are conjunctions of two unary attributes.
In order to solve the FSAL task, the learner must correctly determine the context. Just like in zero-shot learning, one natural way to solve this problem would be to learn to predict the underlying attributes of each image. Given the attributes, you could then estimate the context in each episode (Lampert et al., 2014). However, methods that accurately predict attributes relevant to training episodes may not generalize well, since at test time FSAL introduces novel attributes. Instead, we explore methods that allow more general representations to be learned.
3 Experiment Methodology
In this section, we describe a range of methods that can be used for the problem of few-shot attribute learning. The methods can be organized into two stages. The first stage is representation learning through either pre-training the network or performing meta-learning. The second stage is learning a few-shot classifier at test-time to solve a new episode. We describe each stage of learning below.
3.1 Stage I: Representation Learning
We consider the following representation approaches in our evaluation.
Supervised:
Many of the existing few-shot learning approaches include a stage of supervised representation learning. Two classes of approaches are frequently employed:
-
Episodic meta-learning approaches train directly from a set of few-shot episodes using episodic labels. This class of methods can be naturally applied to our learning setting.
-
Supervised classification approaches train a network to directly classify a set of training classes using absolute labels, and at test time, the embedding network is transferred to solve the test task by training another classifier on top. If absolute attributes are provided to the learner, then one natural approach is to instead train an attribute classifier with multiple binary outputs. After the attribute classifier network is learned, we can then transfer the representations to recognize test attributes. We denote this method as Supervised Attributes (SA).
Unsupervised:
As supervised representation learning may not generalize to novel attributes, we also consider unsupervised representation learning as another option. We chose SimCLR (Chen et al., 2020) as a representative from this category due to its empirical success. In general, contrastive learning approaches aim to build invariant representations between a pair of inputs that are produced by applying random data augmentations (e.g. cropping) to an input image. It is likely to preserve more general semantic features since all attributes are useful towards identifying another random crop of the same image. We first obtain the embedding output from the CNN, and then following (Chen et al., 2020), we project to using a multi-layered perceptron (MLP): . With a batch of image pairs denoted by , we can obtain their features , and the contrastive loss function is defined similar to the cross entropy function:
| (3) |
where is a temperature parameter. We denote Unsupervised representation learning as U.
Unsupervised-then-Finetuning:
For unsupervised learning, we also consider adding a subsequent stage of supervised fine-tuning to utilize attribute labels from the training set. Note that fine-tuning here is different from fine-tuning in regular few-shot learning as it is not fine-tuning on test episodes but rather on the original training set. To prevent overwriting the representations and making them overly sensitive to training attributes, we add another projection MLP that learns more specific representations for finetuning on training attributes: Here, we again consider using two different modes of supervision: 1) the FSAL binary episodic labels, or 2) the underlying absolute attribute labels:
-
[leftmargin=*]
-
Unsupervised-then-FineTune-on-Episodes (UFTE). We adopt the Prototypical Networks (Snell et al., 2017) formulation, where the network solves a learning episode of positive and negative support examples by using prototypes : With query example , we can make a binary prediction: where is some dissimilarity score, e.g. Euclidean distance or cosine dissimilarity, and the training objective is to minimize the classification loss between the prediction and the label :
(4) where is the index of query examples.
-
Unsupervised-then-FineTune-on-Attributes (UFTA). With persistent attribute information, we can train a linear classifier with sigmoid activation to directly predict the absolute attribute labels : , with the loss being
(5) where is the index of attributes.
3.2 Stage II: Few-Shot Learning
Once representations are learned, it remains to be decided how to use the small support set of each given test episode in order to make predictions for the associated query set. For each model described in the previous stages, we consider three candidate approaches: nearest neighbor (NN) used in MatchingNet (Vinyals et al., 2016), the nearest centroid (NC) used in ProtoNet (Snell et al., 2017), and logistic regression (LR) used in Chen et al. (2019). The LR approach learns a weight coefficient for each feature dimension, thus performing some level of feature selection, unlike the NC or NN alternatives. In addition, we apply an L1 regularizer on LR to encourage sparsity. In this way, the learning of a classifier is essentially done at the same time as the selection of feature dimensions. The overall objective of the classifier is:
| (6) |
where , and is the representation vector extracted from the CNN backbone. Note that in this stage we discard the projection MLPs that are defined in previous stages since they are trained towards training attributes and self-supervised objectives, and we found that they do not transfer well to novel attributes.
| Paradigm | Test time task | Task specification |
|---|---|---|
| ZSL (Lampert et al., 2014) | Novel semantic classes of existing attributes | Attribute IDs |
| CZSL (Misra et al., 2017) | Novel combinations of existing attributes & classes | Attribute IDs |
| FSL (Lake et al., 2011) | Novel semantic classes | Support examples |
| FSAL (Ours) | Novel (previously unlabeled) attributes | Support examples |
4 Related Work
Few-shot learning:
Few-shot learning (FSL) (Fei-Fei et al., 2006; Lake et al., 2011; Vinyals et al., 2016) entails learning new tasks with only a few examples. With an abundance of training data, FSL is closely related to the general meta-learning or learning to learn paradigm (Thrun, 1998), as a few-shot learning algorithm can be developed on training tasks and run on novel tasks at test time. In standard few-shot classification, each image only has a single unambiguous class label, whereas in our few-shot attribute learning, the target attributes can vary depending on how the support set is presented. We show in this paper that this is a more challenging problem as it requires the model to be more flexible and generalizable. In early benchmarks, a set of semantic classes was randomly split into a training and test set. We hypothesize that this often leads to a common set of attributes that span (most of) the training and test classes, thus causing high transferability between these two sets, which allows simple solutions based on feature re-use (Chen et al., 2019; Raghu et al., 2020) to work well. Later benchmarks explicitly attempt to vary the separation between train and test classes, based on varying the distances in the underlying WordNet classes (tiered-ImageNet (Ren et al., 2018)), or in different image domains (Meta-Dataset (Triantafillou et al., 2020)). However, we argue that reasoning about the underlying attributes directly offers a more systematic framework to measure the relatedness and transferability between the train and test set. We expect our analysis to open the door to such studies in the future. Few-shot attribute learning is also related to multi-label few-shot learning (Alfassy et al., 2019; Li et al., 2021) and compositional few-shot learning (Tokmakov et al., 2019). These prior works emphasize on the compositional aspect, whereas we propose models that address the transferability of the learned representations. Additionally, Xiang et al. (2019) explored combining incremental few-shot learning and attribute learning for pedestrian images.
Attribute learning:
In the past, there have been a number of works that aim to predict attribute information from raw inputs (Ferrari and Zisserman, 2007; Farhadi et al., 2009, 2010; Wang and Mori, 2010). A related model is later proposed by Koh et al. (2020) to achieve better causal interpretability.There have also been a number of datasets that have been collected with visual attributes annotated (Welinder et al., 2010; Yu and Grauman, 2014; Liu et al., 2015; Patterson and Hays, 2016; Pham et al., 2021). One key difference between our work and these attribute learning approaches is that at test time we aim to learn a classifier on novel attributes that are previously not labeled in the training set, and this brings additional challenges of transfer learning and learning with limited labeled data.
Zero-shot learning:
In zero-shot learning (ZSL) (Farhadi et al., 2009; Akata et al., 2013; Xian et al., 2019; Lampert et al., 2014; Romera-Paredes and Torr, 2015; Akata et al., 2015), a model is asked to recognize classes not present in the training set, supervised only by some auxiliary description (Ba et al., 2015) or attribute values (Farhadi et al., 2009) (see Wang et al. (2019a) for a survey). Lampert et al. (2014) studied the direct attribute prediction method, similar to the Supervised Attribute baseline described in Section 5.2. Compositional ZSL aims at learning classes (Misra et al., 2017; Purushwalkam et al., 2019; Wang et al., 2019b; Yang et al., 2020) defined by a novel composition of labeled attributes and object classes. An important distinction between ZSL and our few-shot attribute learning task is that ZSL uses the same set of attributes for both training and testing; by contrast, our task asks the model to learn attributes for which there are no labels during training, and they may not be relevant to any of the training attributes or episodes. We summarize the relationships between ZSL, FSL and our task in Table 1.
Generalization to novel tasks:
One key component of our work is an attempt to understand the generalization behavior of learning novel concepts at test time. Relevant theoretical studies consider novel task generalization, casting it in a transfer learning and learning to learn framework (Baxter, 2000; Ben-David and Borbely, 2008; Ben-David et al., 2010; Pentina and Lampert, 2014; Amit and Meir, 2018; Lucas et al., 2021). A common theme in these studies is in characterizing task relatedness, and the role that it plays in generalization to novel tasks. Arnold and Sha (2021) studied task clustering for few-shot learning in the embedding space and found class splits that are of different difficulty levels. Sariyildiz et al. (2021) use the WordNet hierarchy to compute semantic distances. In our paper, we instead split the data in the attribute space, and if we assume that semantic classes are combinations of attributes, then a disjoint attribute split will imply further semantic distances. In our work, we investigate the role of task relatedness empirically by investigating generalization performance under different splits of the attribute space.
| Celeb-A | Zappos-50K | ||||
| Sup. | 5-shot | 20-shot | 5-shot | 20-shot | |
| Chance | - | 50.000.00 | 50.000.00 | 50.000.00 | 50.000.00 |
| MatchingNet | E | 68.300.76 | 71.730.52 | 77.260.60 | 80.470.49 |
| MAML/ANIL | E | 71.240.74 | 73.350.53 | 77.050.50 | 81.100.43 |
| TAFENet | E | 69.100.76 | 72.110.54 | 79.200.57 | 83.420.44 |
| ProtoNet | E | 72.120.75 | 75.270.51 | 77.220.51 | 83.420.41 |
| TADAM | E | 73.540.70 | 76.060.53 | 81.450.50 | 86.230.40 |
| ID | C | 69.950.69 | 77.530.53 | - | - |
| SA | A | 72.910.74 | 78.860.48 | 82.170.48 | 88.240.37 |
| U | - | 73.470.68 | 79.970.51 | 83.880.44 | 90.920.32 |
| UFTE | E | 76.690.69 | 82.830.48 | 85.500.42 | 92.200.28 |
| UFTA | A | 78.980.69 | 84.140.48 | 84.610.43 | 91.660.29 |
| Oracles | |||||
| SA* | A* | 84.740.60 | 89.150.38 | 88.110.39 | 93.000.28 |
| GT | - | 91.070.49 | 98.160.17 | 97.660.16 | 99.840.04 |
5 Experiments
In this section, we evaluate different representation and few-shot learning approaches on FSAL using several datasets.
5.1 Datasets
We consider the following three datasets:
-
Celeb-A (Liu et al., 2015) contains over 200K images of faces. Each image is annotated with binary attributes, detailing hair color, facial expressions, etc. We split 14 attributes for training and 13 for test.
-
Zappos-50K (Yu and Grauman, 2014) contains just under 50K images of shoes annotated with attribute values. We split these into 40 attribute values for training, and 39 for testing.
-
ImageNet-with-Attributes is a small subset of the ImageNet dataset (Deng et al., 2009) with attribute annotations. It has 9.6K images. We used 11 attributes for training and 10 for testing. Note that this subset of ImageNet that has attribute labels is significantly smaller than the two datasets above, and it is not sufficiently large for meta-learning methods from scratch. Hence, the results for this dataset are reported separately.
In all of the datasets above, there is no overlap between training and test attributes. Additional split details can be found in the supplementary materials.
Episode construction:
For each episode, we randomly select one or two attributes and look for positive examples belonging to these attributes simultaneously. We also sample an equal number of negative examples that don’t match the selected attributes. This will construct a support set of positive and negative samples, and then we repeat the same process for the corresponding query set as well. Sample episodes are shown in Figure 1. Additional episodes are shown in the Appendix.
| Celeb-A | Zappos-50K | |||||
|---|---|---|---|---|---|---|
| NN | NC | LR | NN | NC | LR | |
| Meta | 71.730.52 | 75.270.51 | 73.380.53 | 80.470.49 | 83.420.41 | 81.100.43 |
| SA | 75.330.47 | 77.240.51 | 78.860.48 | 81.170.44 | 85.480.41 | 88.240.37 |
| U | 75.720.48 | 77.780.52 | 79.970.51 | 85.170.40 | 88.630.37 | 90.920.32 |
| UFTE | 79.030.47 | 81.040.47 | 82.830.48 | 86.230.34 | 90.610.31 | 92.200.28 |
| UFTA | 77.300.52 | 82.160.46 | 84.140.48 | 86.40 0.36 | 90.250.33 | 91.660.29 |
| SA* | 78.840.41 | 84.610.42 | 89.150.38 | 87.540.33 | 90.970.31 | 93.000.28 |
| Celeb-A | Zappos-50K | |||||
|---|---|---|---|---|---|---|
| Train attr | Test attr | Gap | Train attr | Test attr | Gap | |
| ProtoNet | 87.120.40 | 75.090.52 | –12.03 | 92.880.24 | 83.420.41 | –9.46 |
| SA | 88.250.38 | 78.860.48 | –9.39 | 95.110.19 | 88.240.37 | –6.87 |
| U | 79.480.54 | 79.970.51 | –0.49 | 94.030.23 | 90.920.32 | –3.11 |
| UFTE | 87.250.40 | 82.830.48 | –4.42 | 95.910.18 | 92.200.28 | –3.71 |
| UFTA | 85.530.43 | 84.140.48 | –1.39 | 94.610.21 | 91.660.29 | –2.95 |
| SA* | 87.880.39 | 89.150.38 | +1.27 | 95.590.18 | 93.000.28 | –2.58 |
| L | D? | UFTE | UFTA | ||
|---|---|---|---|---|---|
| Val Acc. () | Gap | Val Acc. () | Gap | ||
| 0 | 78.02 (–2.19) | –9.72 | 82.81 (+2.60) | –4.80 | |
| 1 | 76.86 (–3.35) | –11.14 | 79.56 (–0.65) | –7.43 | |
| 1 | ✓ | 82.01 (+1.80) | –5.63 | 83.39 (+3.18) | –2.05 |
| 2 | 76.32 (–3.89) | –11.58 | 79.71 (–0.50) | –7.23 | |
| 2 | ✓ | 82.43 (+2.22) | –4.83 | 83.86 (+3.65) | –1.90 |
5.2 Methods for Comparison
As outlined in Section 3, we consider the following representation learning and finetuning methods:
-
ID trains a network to perform the auxiliary task of face identity classification (Celeb-A only).
-
SA, or supervised attribute, resembles the “Baseline” approach in the FSL literature (Chen et al., 2019). The network learns representations by predicting the training attributes associated with each image.
-
U denotes unsupervised representation learning (SimCLR). We train separate models on the Celeb-A and Zappos datasets. For ImageNet, we utilize the off-the-shelf model checkpoint trained on the full ImageNet-1K.
-
UFTE/UFTA as explained in Section 3.1, we evaluate UFTE and UFTA which finetune on training episodes and training attributes respectively.
In addtion, we also consider a set of classic few-shot and meta-learning methods. These methods are directly trained on FSAL episodes of training attributes.
-
MatchingNet (Vinyals et al., 2016) is a soft version of 1-nearest-neighbor. At test time, it will retrieve the label of the closest support example in the feature space.
-
ProtoNet (Snell et al., 2017) computes an average “prototype” for each class and retrieves the closest one.
-
TAFENet (Wang et al., 2019c) learns a meta-network that can output task-conditioned classifier parameters.
-
TADAM (Oreshkin et al., 2018) predicts the batch normalization parameters by using the average features of the episode. For our task we found that conditioning on the positive examples only works the best.
In addition to the approaches above, we also provide two oracle approaches to study the upper bound to generalization to novel attributes.
-
Oracle SA* learns its representations by predicting all binary attributes including both training and test ones.
-
Oracle GT directly uses the ground-truth binary attribute values as input features, and the readout is performed by training a logistic regression. It still needs to select the active attributes that are used in each episode.
For the few-shot learning stage, as explained in Section 3.2, we mainly use logistic regression (LR) in few-shot episodes, but we also report results using the nearest neighbor (NN) and nearest centroid (NC) classifiers. Note that the few-shot classifiers can be composed with any of the above representation learning methods (e.g. SA, U, UFTE, UFTA, etc.).
Implementation details:
For Celeb-A and Zappos, images were cropped and resized to 8484. We used ResNet-12 (He et al., 2016; Oreshkin et al., 2018) as the CNN backbone. The projection MLPs have 512-512-128 units. We train SimCLR entirely on Celeb-A/Zappos images, i.e. not using pre-trained ImageNet checkpoints for fair comparison. For ImageNet-with-Attributes, we utilize the off-the-self SimCLR model from ImageNet-1k, which has access to more unlabeled images. The image dimensions are 224224. Additional details are in the Appendix.
| ImageNet-with-Attributes | ||||
|---|---|---|---|---|
| X | A | 5-shot | 20-shot | |
| Chance | 50.00 0.00 | 50.00 0.00 | ||
| MAML | 57.90 0.75 | 57.46 0.70 | ||
| U | ✓ | 69.05 0.65 | 71.25 0.62 | |
| SA | ✓ | 64.36 0.68 | 64.16 0.65 | |
| UFTE | ✓ | 70.92 0.69 | 72.12 0.63 | |
| UFTA | ✓ | ✓ | 71.12 0.65 | 72.91 0.63 |
| NN | NC | LR | |
|---|---|---|---|
| Meta | 61.28 0.62 | 61.50 0.70 | 57.46 0.70 |
| U | 69.63 0.59 | 71.12 0.66 | 71.25 0.62 |
| SA | 62.42 0.62 | 62.84 0.68 | 64.16 0.65 |
| UFTE | 69.77 0.57 | 72.94 0.61 | 72.12 0.63 |
| UFTA | 71.55 0.61 | 72.42 0.63 | 72.91 0.63 |
| SA* | 68.36 0.60 | 70.48 0.66 | 70.92 0.64 |
| Train | Test | Gap | |
|---|---|---|---|
| attr | attr | ||
| MAML | 68.16 0.59 | 57.46 0.70 | -10.70 |
| U | 76.36 0.60 | 71.25 0.62 | -5.11 |
| SA | 69.03 0.66 | 64.16 0.65 | -4.87 |
| UFTE | 78.31 0.56 | 72.12 0.63 | -6.19 |
| UFTA | 77.08 0.62 | 72.91 0.63 | -4.17 |
| SA* | 68.72 0.64 | 70.92 0.64 | 2.20 |

5.3 Comparing Various Methods for FSAL
Table 2 shows our main results on Celeb-A and Zappos-50K with 5- and 20-shot episodes. Table 3 explores different combinations of representations and few-shot learners. Overall, the standard episodic meta-learners performed relatively poorly. Also, supervised attribute (SA) learning and learning via the auxiliary task of class facial identification (ID) were not helpful for representation learning either. Interestingly, U attained relatively better test performance, suggesting that the training objective in contrastive learning indeed preserves more general features—not just for semantic classification tasks as shown in prior work, but also for the flexibly-defined attribute classes in our FSAL paradigm. All these evidences suggest that unsupervised representation learning is better than supervised methods for FSAL.
Moreover, UFTA and UFTE approaches obtained significant gains in performance, suggesting that a combination of unsupervised features with some supervised information is indeed beneficial for this task. Lastly, they are able to reduce the generalization gap between SA and the oracle SA*, in fact almost closing it entirely on Zappos-50K. We investigate and analyze the benefit of unsupervised pretraining and supervised finetuning further in Section 5.4.
Results on ImageNet-with-Attributes are reported separately for clarity, because U, UFTE, and UFTA had access to additional unlabeled examples. As shown in Table 6, both UFTE and UFTA outperformed other methods substantially. Because of the additional unlabeled data available in this setting, even U achieved a substantially better accuracy than SA and MAML. Results in Table 7 show that UFTE and UFTA work well when combined with different few-shot learners.
Visualizing few-shot classifiers:
To understand and interpret the decision made by few-shot linear classifiers, we visualize the classifier weights by using CAM (Zhou et al., 2016), and plot the heatmap over the 1111 spatial feature map in Figure 2. SA sometimes shows incorrect localization as it is not trained to classify those novel test attributes. SA* shows bigger but less precise heatmaps since the training objective encourages the propagation of attribute information spatially. In contrast, UFTA produces accurate and localized heatmaps that pinpoint the location of the attributes (e.g. mustache or cheekbone); this is impressive since no labeled information concerning these attributes was available during representation pre-training and finetuning. This result supports the hypothesis that local features can be good descriptors that match different views of the same instance during contrastive learning, and finetuning further establishes a positive transfer between training and test attributes.
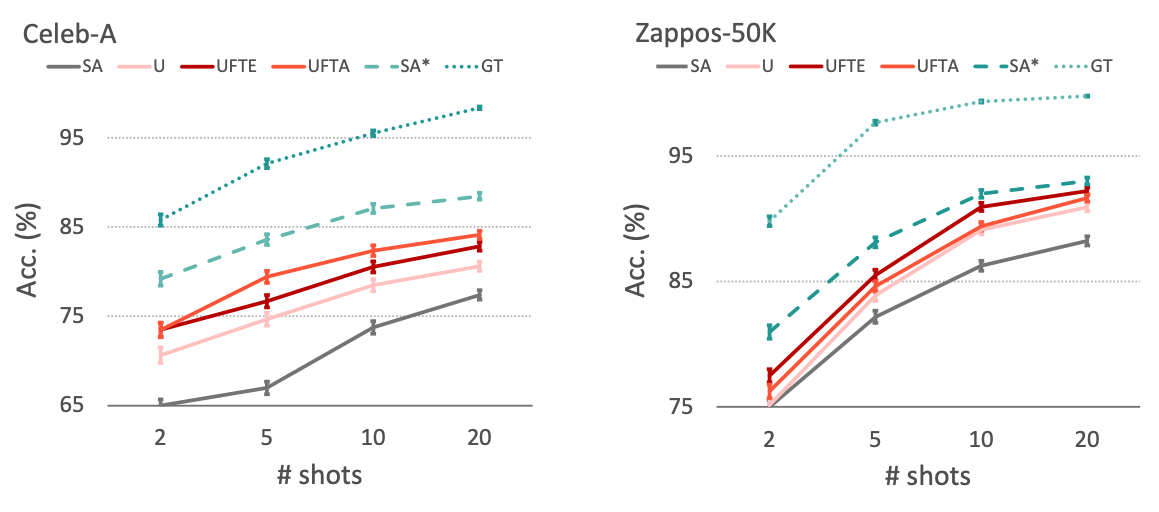
Number of shots and task ambiguity:
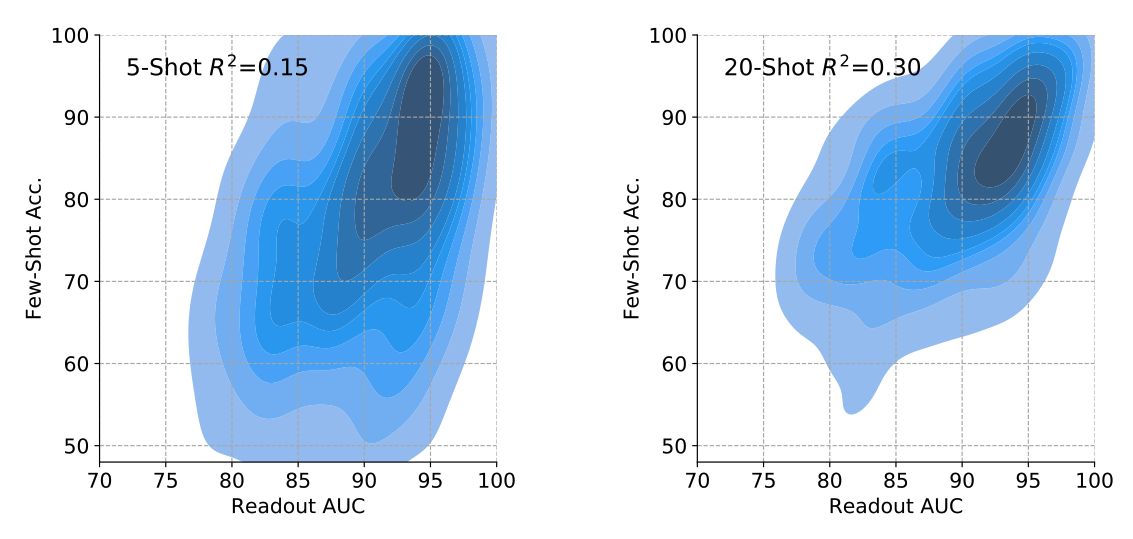
Our few-shot attribute learning episodes can be ambiguous. For example, by presenting only a smiling face with eyeglasses in the support set, it is unclear whether the positive set is determined by “smiling” or “wearing eyeglasses”. Figure 3 show several approaches evaluated using LR with varying numbers of support examples per class in Celeb-A and Zappos-50K episodes, respectively. The oracle GT gradually approached 100% accuracy as the number of shots approached 20. This demonstrates that FSAL tasks potentially require more support examples than standard FSL to resolve ambiguity. Again here, UFTA and UFTE consistently outperformed U, SA, and ID across different number of shots. Figure 4 shows the correlation between readout performance of attributes and few-shot learning accuracy, using UFTA. With a larger number of shots, there is a higher correlation between the two, but there is still a large amount of variance that is due to the ambiguity of the task itself. More details are included in the Appendix.
Ablation studies:
Table 5 studies the effect of the projection MLP for attribute classification finetuning. Adding MLP projection layers was found to be beneficial for unsupervised learning in prior work (Chen et al., 2020). Here we found that adding MLP layers is also critical in supervised finetuning. Finetuning directly on the backbone (depth=0), and keeping the MLP during test (Discard=no) both led to significant drop in performance. In the Appendix, we also report on studies of the effect of adding the L1 regularizer on LR.
5.4 Analysis of Few-Shot Generalization
In Tables 4 and 8, we study the performance gap between training attributes and test attributes. Notably, SA performs very well on test episodes defined using training attributes, but there is a large generalization gap between training and test attributes. UFTE and UFTA show significant improvements in terms of reducing the generalization gap between training and test attributes. Moreover, we find that self-supervised pre-training generally preserves informative features and is more general than supervised pre-training.
Investigating the cause of generalization issues:
We hypothesize that the weak performance of episodic learners and SA on our benchmarks is because their training objectives essentially encourage ignoring attributes that are not useful at training time, but may still be useful at test time. In Appendix G, we study a synthetic problem to further analyze these generalization issues. We explore training a ProtoNet model on data from a linear generative model, where each FSAL episode presents ambiguity in identifying the relevant attributes. In this setting, the network is forced to discard information that is useful for test tasks to solve the training tasks effectively, and thus fails to generalize.
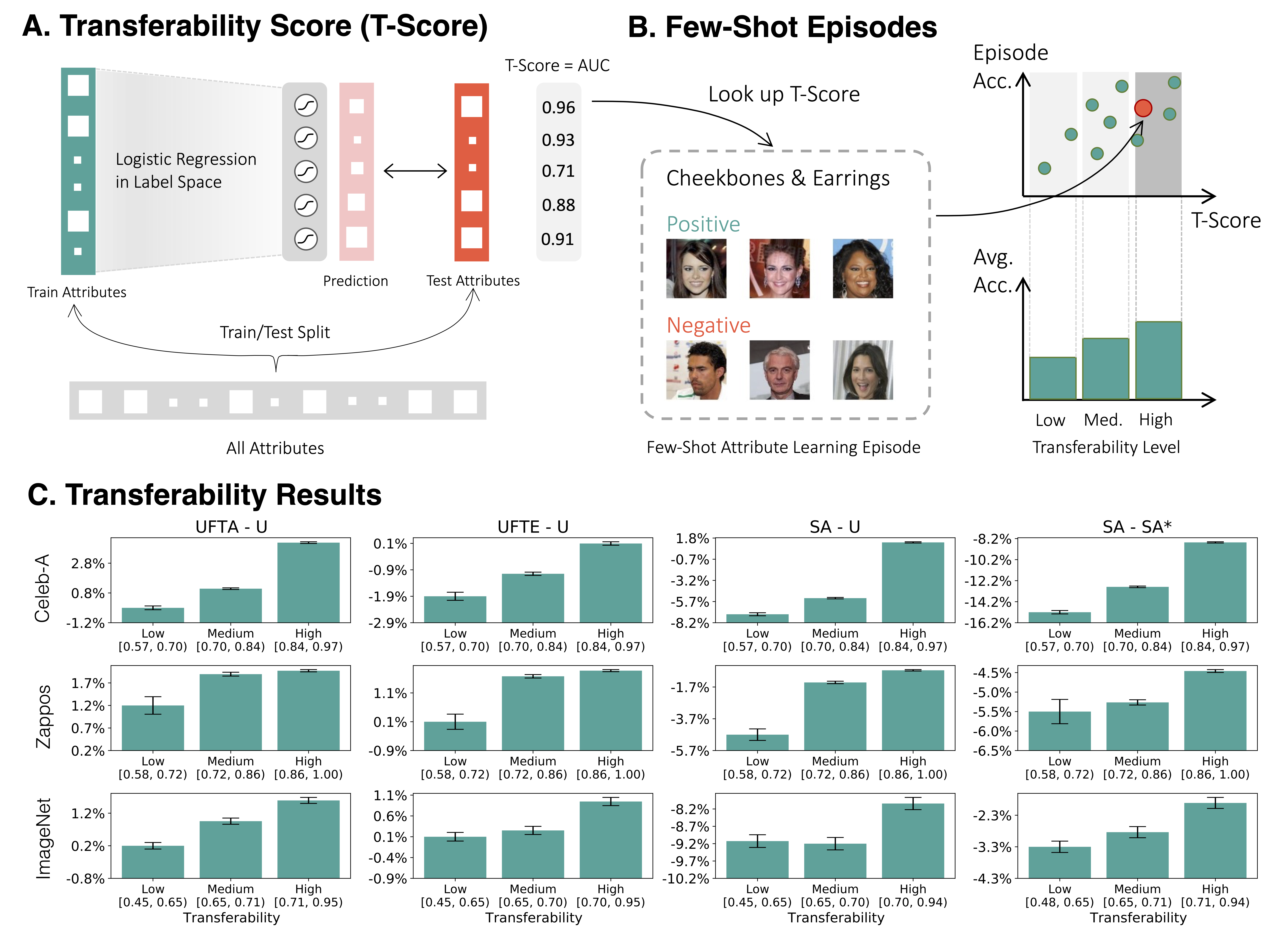
Transferability score:
We aim to investigate the question of why unsupervised pretraining and supervised finetuning produce better performance, and whether the performance difference is caused by the closeness between training and test attributes. More concretely, we aim to predict the transferability between training and test splits by analyzing the training vs. test attributes. Each image has a complete attribute vector, describing the values of each attribute in the image. Some of these attributes are in the training set, and others in the test set. To quantify the transferability, we leverage the idea of mutual information. In particular, we learn a logistic regression model that takes the training attribute vector in a particular image as input and predicts the value of one of the test attributes in that image. Each logistic regression model will generate an AUC score on held-out images, and we average them across the relevant test attributes in each episode, and we define this AUC score as the “transferability score.” Our hypothesis is that more mutual information between the attribute label distributions will translate to higher transfer performance.
In Figure 5, we ran experiments using 100 random splits of training and test attributes. The results verify our hypothesis. We see positive correlation between the transfer performance and our transferability score: When subtracting U as a baseline, both UFTA and UFTE models get better when there is higher transferability (subtraction reduces the effect of per-episode variability). The same conclusion can be drawn when we subtract SA* from SA. By plotting the relation between U and SA, we show that supervised learning is more helpful when there is higher transferability in the label space whereas self-supervised learning is more flexible at adapting to novel target tasks.
To summarize, our empirical evidence suggests that unsupervised representation learning is superior to supervised methods in terms of retaining information relevant to the test attributes. Other methods, such as supervised representation learning or episodic training, tend to effectively ignore attributes that were not used for labelling during training. Moreover, supervised finetuning of the representations is helpful when the transferability between test and train attributes is high, but less so otherwise, and supervised pretraining alone is harmful to novel attribute generalization for most train vs. test attribute pairs.
6 Conclusion
To investigate few-shot generalization, we developed FSAL, a novel few-shot learning paradigm that requires learners to generalize to novel attributes at test time. We developed benchmarks using the Celeb-A, Zappos-50K, and ImageNet datasets to create learning episodes using existing attribute labels. This setting presents a strong generalization challenge, since the split in attribute space can make the training and test tasks less similar than traditional few-shot learning tasks. Consequently, standard supervised representation learning performs poorly on the test set, unlike recent benchmark results in few-shot learning of semantic classes. However, unsupervised contrastive learning preserved more general features, and further finetuning yielded strong performance. We also studied the performance gap under different splits in the attribute label space where we found that supervised representation learning works better when there is more information shared between train and test attributes.
Limitations:
Our empirical analysis could be made more complete by including other unsupervised representation learning methods and extending to other domains. Further, the episodes contained in our benchmark tasks can sometimes be difficult for humans to resolve even after we removed ambiguous attributes.
Societal Impact:
FSAL relies on attribute labels, which can be difficult to obtain and encode bias in some settings (e.g. the attractive attribute in Celeb-A).
Contribution Statement
All authors contributed to the high-level idea and writing of the paper. MR contributed to the code base for running attribute-based few-shot learning experiments, discovered that unsupervised learning plus finetuning is beneficial, performed experiments on Celeb-A, and created most of the figures and graphics. ET helped with figure creation, implemented the flexible few-shot version of Zappos-50K and ran the experiments on that dataset. KCW contributed to the FFSL task definition, implemented the ImageNet-with-Attributes FFSL benchmark, and the associated code for using the off-the-shelf models. JL designed and implemented early experiments in the FFSL setting, provided the formal description of FFSL, and analyzed the linear toy problem presented in Appendix E. JS contributed to the analysis of early FFSL experiments. XP and AT contributed ideas about the underlying question and its possible solutions, and helped interpret results. RZ contributed many ideas behind the underlying question studied here and the problem formulation, and led the team’s brainstorming about how to test the hypotheses, the datasets and benchmarks, and modeling approaches and visualizations.
Acknowledgments
We would like to thank Claudio Michaelis for several helpful discussions about the problem formulation, Alireza Makhzani for related generative modeling ideas, and Mike Mozer for discussions about contextual similarity. Resources used in preparing this research were provided, in part, by the Province of Ontario, the Government of Canada through CIFAR, and companies sponsoring the Vector Institute (www.vectorinstitute.ai/#partners). This project is supported by NSERC and the Intelligence Advanced Research Projects Activity (IARPA) via Department of Interior/Interior Business Center (DoI/IBC) contract number D16PC00003. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. Disclaimer: The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of IARPA, DoI/IBC, or the U.S. Government.
References
- Label-embedding for attribute-based classification. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- Evaluation of output embeddings for fine-grained image classification. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- LaSO: label-set operations networks for multi-label few-shot learning. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- Meta-learning by adjusting priors based on extended pac-bayes theory. In Proceedings of the 35th International Conference on Machine Learning, ICML, J. G. Dy and A. Krause (Eds.), Cited by: §4.
- Embedding adaptation is still needed for few-shot learning. CoRR abs/2104.07255. Cited by: §1, §4.
- Predicting deep zero-shot convolutional neural networks using textual descriptions. In IEEE International Conference on Computer Vision, ICCV, Cited by: §4.
- A model of inductive bias learning. Journal of artificial intelligence research 12, pp. 149–198. Cited by: §4.
- A theory of learning from different domains. Machine learning 79 (1-2), pp. 151–175. Cited by: §4.
- A notion of task relatedness yielding provable multiple-task learning guarantees. Machine learning 73 (3), pp. 273–287. Cited by: §4.
- A simple framework for contrastive learning of visual representations. CoRR abs/2002.05709. Cited by: §3.1, §5.3.
- A closer look at few-shot classification. In Proceedings of the 7th International Conference on Learning Representations, ICLR, Cited by: §1, §3.2, §4, 2nd item.
- Imagenet: a large-scale hierarchical image database. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: 3rd item.
- Describing objects by their attributes. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4, §4.
- Attribute-centric recognition for cross-category generalization. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- One-shot learning of object categories. IEEE TPAMI 28 (4), pp. 594–611. Cited by: §4.
- Learning visual attributes. In Advances in Neural Information Processing Systems 20, NIPS, Cited by: §4.
- Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, ICML, Cited by: 2nd item.
- A broader study of cross-domain few-shot learning. In 14th European Conference on Computer Vision, ECCV, Cited by: §1.
- Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §5.2.
- Concept bottleneck models. In Proceedings of the 37th International Conference on Machine Learning, ICML, Cited by: §4.
- One shot learning of simple visual concepts. In Proceedings of the 33th Annual Meeting of the Cognitive Science Society, CogSci, Cited by: §1, Table 1, §4.
- Attribute-based classification for zero-shot visual object categorization. IEEE Trans. Pattern Anal. Mach. Intell. 36 (3), pp. 453–465. Cited by: §2, Table 1, §4.
- Compositional embeddings for multi-label one-shot learning. In IEEE Winter Conference on Applications of Computer Vision, WACV, Cited by: §4.
- Deep learning face attributes in the wild. In Proceedings of International Conference on Computer Vision, ICCV, Cited by: §4, 1st item.
- Theoretical bounds on estimation error for meta-learning. Cited by: §4.
- From red wine to red tomato: composition with context. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: Table 1, §4.
- TADAM: task dependent adaptive metric for improved few-shot learning. In Advances in Neural Information Processing Systems 31, NeurIPS, Cited by: 5th item, §5.2.
- COCO attributes: attributes for people, animals, and objects. In 14th European Conference Computer Vision, ECCV, B. Leibe, J. Matas, N. Sebe, and M. Welling (Eds.), Cited by: §4.
- A pac-bayesian bound for lifelong learning. In Proceedings of the 31th International Conference on Machine Learning, ICML, Cited by: §4.
- Learning to predict visual attributes in the wild. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- Task-driven modular networks for zero-shot compositional learning. In IEEE/CVF International Conference on Computer Vision, ICCV, Cited by: §4.
- Rapid learning or feature reuse? towards understanding the effectiveness of MAML. In 8th International Conference on Learning Representations, ICLR, Cited by: §4, 2nd item.
- Meta-learning for semi-supervised few-shot classification. In Proceedings of 6th International Conference on Learning Representations, ICLR, Cited by: §1, §4.
- An embarrassingly simple approach to zero-shot learning. In Proceedings of the 32nd International Conference on Machine Learning, ICML, Cited by: §4.
- Family resemblances: studies in the internal structure of categories. Cognitive psychology 7 (4), pp. 573–605. Cited by: §1.
- Concept generalization in visual representation learning. Cited by: §1, §4.
- Prototypical networks for few-shot learning. In Advances in Neural Information Processing Systems 30, NIPS, Cited by: 1st item, §3.2, 3rd item.
- Lifelong learning algorithms. In Learning to learn, pp. 181–209. Cited by: §4.
- Learning compositional representations for few-shot recognition. In 2019 IEEE/CVF International Conference on Computer Vision, ICCV 2019, Seoul, Korea (South), October 27 - November 2, 2019, pp. 6371–6380. External Links: Link, Document Cited by: §4.
- Meta-dataset: a dataset of datasets for learning to learn from few examples. In 8th International Conference on Learning Representations, ICLR, Cited by: §1, §4.
- Matching networks for one shot learning. In Advances in Neural Information Processing Systems 29, NIPS, Cited by: §1, §3.2, §4, 1st item.
- A survey of zero-shot learning: settings, methods, and applications. ACM Transactions on Intelligent Systems and Technology, TIST 10 (2), pp. 1–37. Cited by: §4.
- Task-aware feature generation for zero-shot compositional learning. CoRR abs/1906.04854. Cited by: §4.
- TAFE-net: task-aware feature embeddings for low shot learning. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: 4th item.
- A discriminative latent model of object classes and attributes. In 11th European Conference on Computer Vision, ECCV, Cited by: §4.
- Caltech-ucsd birds 200. Cited by: §4.
- Zero-shot learning - A comprehensive evaluation of the good, the bad and the ugly. IEEE Trans. Pattern Anal. Mach. Intell. 41 (9), pp. 2251–2265. Cited by: §4.
- Incremental few-shot learning for pedestrian attribute recognition. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI, Cited by: §4.
- Learning unseen concepts via hierarchical decomposition and composition. In IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4.
- Fine-grained visual comparisons with local learning. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: §4, 2nd item.
- Learning deep features for discriminative localization. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Cited by: Figure 2, §5.3.
Appendix A Attribute Readout
In Tab. 9 and 11, we provide attribute readout performance with different learned representations. This is a similar task that measures the generalizability, but it does not evaluate the rapid learning aspect brought by few-shot learning.
| Mean AUC | RND | PN | ID | SA | U | UFTE | UFTA | SA* |
|---|---|---|---|---|---|---|---|---|
| All (40) | 79.18 | 88.80 | 91.29 | 90.27 | 92.80 | 93.34 | 93.33 | 94.46 |
| Train+Test (27) | 82.27 | 93.38 | 94.31 | 94.23 | 95.78 | 96.53 | 96.52 | 97.18 |
| Train (14) | 84.40 | 96.04 | 95.34 | 96.04 | 96.43 | 97.23 | 97.23 | 97.50 |
| Test (13) | 79.96 | 90.52 | 93.19 | 92.63 | 95.08 | 95.78 | 95.76 | 96.84 |
Appendix B Ablation studies
Table 10 studies the effect of the L1 regularization. The benefit is especially noticeable on SA* and GT, since it allows the few-shot learner to have a sparse selection of disentangled feature dimensions.
| SA | U | UFTE | UFTA | SA* | GT | |
|---|---|---|---|---|---|---|
| LR | 77.4 | 79.2 | 82.2 | 83.1 | 87.1 | 95.8 |
| +L1 (1e-4) | 77.6 (+0.2) | 79.4 (+1.2) | 82.3 (+0.1) | 83.2 (+0.1) | 87.4 (+0.3) | 96.1 (+0.3) |
| +L1 (1e-3) | 78.2 (+0.8) | 80.2 (+1.0) | 82.4 (+0.2) | 83.8 (+0.7) | 88.4 (+1.3) | 97.1 (+1.3) |
| +L1 (1e-2) | 75.7 (–1.7) | 78.3 (–0.9) | 78.8 (–3.5) | 79.5 (–3.6) | 87.6 (+0.5) | 98.2 (+2.4) |
| Mean AUC | SA | SA* | U | UFTA |
|---|---|---|---|---|
|
All (25 attributes) |
72.01 | 73.02 | 81.08 | 82.49 |
| Train+Test (21 attributes) | 73.43 | 78.98 | 80.14 | 82.37 |
| Train (11 attributes) | 72.69 | 75.86 | 80.63 | 82.43 |
| Test (10 attributes) | 72.01 | 74.98 | 81.08 | 83.30 |
Appendix C Additional heatmap visualization
We provide additional visualization results in Figure 6, 7, and 8, and we plot the heat map to visualize the LR classifier weights. Figure 6 includes SA*, U, and UFTE which are omitted in the main paper due to space limitations. Figure 7 and 8 visualize more information including both support and query examples in the episode, and some of the episodes are challenging to solve given just a few examples.



| Train | 5_o_Clock_Shadow | Black_Hair | Blond_Hair | Chubby |
|---|---|---|---|---|
| Double_Chin | Eyeglasses | Goatee | Gray_Hair | |
| Male | No_Beard | Pale_Skin | Receding_Hairline | |
| Rosy_Cheeks | Smiling | |||
| Val/Test | Bald | Bangs | Brown_Hair | Heavy_Makeup |
| High_Cheekbones | Mouth_Slightly_Open | Mustache | Narrow_Eyes | |
| Sideburns | Wearing_Earrings | Wearing_Hat | Wearing_Lipstick | |
| Wearing_Necktie |
Appendix D Attribute splits of Celeb-A
We include the attribute split for Celeb-A in Table 12. There are 14 attributes in training and 13 attributes in val/test. We discarded the rest of the 13 attributes in the original datasets since they are either hard to classify with the oracle classifier (e.g. big lips, oval face) or simply ambiguous (e.g. young, attractive).
| Train | Category-Shoes | Category-Sandals | SubCategory-Oxfords | SubCategory-Heel |
|---|---|---|---|---|
| SubCategory-Boot | SubCategory-Slipper Flats | SubCategory-Short heel | SubCategory-Flats | |
| SubCategory-Slipper Heels | SubCategory-Athletic | SubCategory-Knee High | SubCategory-Crib Shoes | |
| SubCategory-Over the Knee | HeelHeight-High heel | Closure-Pull-on | Closure-Ankle Strap | |
| Closure-Zipper | Closure-Elastic Gore | Closure-Sling Back | Closure-Toggle | |
| Closure-Snap | Closure-T-Strap | Closure-Spat Strap | Gender-Men | |
| Gender-Boys | Material-Rubber | Material-Wool | Material-Silk | |
| Material-Aluminum | Material-Plastic | Toestyle-Capped Toe | Toestyle-Square Toe | |
| Toestyle-Snub Toe | Toestyle-Bicycle Toe | Toestyle-Open Toe | Toestyle-Pointed Toe | |
| Toestyle-Almond | Toestyle-Apron Toe | Toestyle-Snip Toe | Toestyle-Medallion | |
|
Val/Test |
Category-Boots | Category-Slippers | SubCategory-Mid-Calf | SubCategory-Ankle |
| SubCategory-Loafers | SubCategory-Boat Shoes | SubCategory-Clogs and Mules | SubCategory-Sneakers and Athletic Shoes | |
| SubCategory-Heels | SubCategory-Prewalker | SubCategory-Prewalker Boots | SubCategory-Firstwalker | |
| HeelHeight-Short heel | Closure-Lace up | Closure-Buckle | Closure-Hook and Loop | |
| Closure-Slip-On | Closure-Ankle Wrap | Closure-Bungee | Closure-Adjustable | |
| Closure-Button Loop | Closure-Monk Strap | Closure-Belt | Gender-Women | |
| Gender-Girls | Material-Suede | Material-Snakeskin | Material-Corduroy | |
| Material-Horse Hair | Material-Stingray | Toestyle-Round Toe | Toestyle-Closed Toe | |
| Toestyle-Moc Toe | Toestyle-Wingtip | Toestyle-Center Seam | Toestyle-Algonquin | |
| Toestyle-Bump Toe | Toestyle-Wide Toe Box | Toestyle-Peep Toe |
Appendix E Attribute splits of Zappos-50K
The Zappos-50K dataset annotates images with different values relating to the following aspects of shoes: ‘Category’, ‘Subcategory’, ‘HeelHeight’, ‘Insole’, ‘Closure’, ‘Gender’, ‘Material’ and ‘Toestyle’.
We discarded the ‘Insole’ values, since those refer to the inside part of the shoe which isn’t visible in the images. We also discarded some ‘Material’ values that we deemed hard to recognize visually. We also modified the values of ‘HeelHeight’ which originally was different ranges of cm of the height of the heel of each shoe. Instead, we divided those values into only two groups: ‘short heel’ and ‘high heel’, to avoid having to perform very fine-grained heel height recognition which we deemed was too difficult.
These modifications leave us with a total of 79 values (across all higher-level categories). Not all images are tagged with a value from each category, while some are even tagged with more than one value from the same category (e.g. two different materials used in different parts of the shoe). We split these values into 40 ‘training attributes’ and 39 ‘val/test attributes’.
We include the complete list of attributes in Table 13. The format we use is ‘X-Y’ where X stands for the category (e.g. ‘Material’) and Y stands for the value of that category (e.g. ‘Wool’). We do this to avoid ambiguity, since it may happen that different categories have some value names in common, e.g. ‘Short Heel’ is a value of both ‘SubCategory’ and ‘HeelHeight’.
| Train | pink | spotted | wet | blue |
|---|---|---|---|---|
| shiny | rough | striped | white | |
| metallic | wooden | gray | ||
| Val/Test | brown | green | violet | red |
| orange | yellow | furry | black | |
| vegetation | smooth |
Appendix F Attribute splits of ImageNet-with-Attributes
We include the attribute split for ImageNet-with-Attributes in Table 14. There are 11 attributes in training and 10 attributes in val/test. We discarded the rest of the 4 attributes in the “shape” category (long, round, rectangular and square), since they are difficult to predict from the images.
Appendix G Few-Shot Attribute Learning Toy Problem
In this section, we present a toy problem that illustrates the challenges introduced by the FSAL setting and the failures of existing approaches on this task. This simple problem captures the core elements of our FSAL tasks, including ambiguity, introducing novel attributes at test time, and the role of learning good representations. The primary limitation of this model is the fact that it is fully linear and the attribute values are independent—in a more realistic FSAL task recovering a good representation from the data is significantly more challenging, and the data points will have a more complex relationship with the attributes as in our benchmark datasets.
Problem setup
We define a FSAL problem where the data points are generated from binary attribute strings, , with for some matrix with full column rank and noise source . Thus, each data point is a sum of columns of with some additive noise.
In each episode, examples are labelled as positive when two designated entries of the attribute strings are both 1-valued, and negative otherwise. For the training episodes, the labels depend only on the first entries of . At test time, the labels depend on the remaining attributes. The training and test episodes are generated by choosing two of the attributes in the respective sets. Then data points are sampled with positive labels (the two attributes are 1-valued) and with negative labels (at least one of the attributes is 0-valued).

Linear prototypical network
Now, consider training a prototypical network on this data with a linear embedding network, . Within each episode, the prototypical network computes the prototypes for the positive and negative examples,
where is the set of data points in the episode with label , and is the column of the matrix . Further, the prototypical network likelihood is given by,
The goal of the prototypical network is thus to learn weights that lead to small distances between data points in the same class and large distances otherwise. In the FSAL tasks, there is an additional challenge in that class boundaries shift between episodes. The context (the choice of attribute entries) defining the boundary is unknown and must be inferred from the episode. However, with few shots (small ) there is ambiguity in the correct context — with a high probability that several possible contexts provide valid explanations for the observed data.
Fitting the prototypical network
Notice that under our generative model, with and for we have,
Notice that if , the kernel of , then the entire first term is zero. Further, if (the same class as the prototype) then there is no contribution from the positive attribute features in this term. Otherwise, this term is guaranteed to have some contribution from the positive attribute features.
Therefore, if projects to the linear space spanned by the positive attribute features then is zero when and non-zero otherwise. This means that the model will be able to solve the episode without contextual ambiguity. Then the optimal weights are those that project to the set of features used in the training set—destroying all information about the test attributes which would otherwise introduce ambiguity.
We observed this effect empirically in Figure 9, where we have plotted the matrix . Each column of these plots represents a column of mapped to the prototypical network’s embedding space. The first 5 columns correspond to attributes used at training time, and the remaining 5 to those used at test time.
In the FSAL task described above, as our analysis suggests, the learned prototypical feature weights project out the features used at test time (the last 5 columns). As a result, the model achieved 100% training accuracy but only 51% test accuracy (chance is 50%).
We also compared against an equivalent problem set up that resembles the standard few-shot learning setting. In the FSL problem, the binary attribute strings may have only a single non-zero entry and each episode is a binary classification problem where the learner must distinguish between two classes. Now the vector is a one-hot encoding and the comparison to the prototypes occurs only over a single feature column of , thus there is no benefit to projecting out the test features. As expected, the model we learned (Figure 9 B) is not forced to throw away test-time information and achieves 100% training accuracy and 99% test accuracy.
Settings for Figure 9
We use 10 attributes, 5 of which are used for training and 5 for testing. We use a uniformly random sampled and the prototypical network learns . We use additive Gaussian noise when sampling data points with a standard deviation of 0.1. The models are trained with the Adam optimizer using default settings over a total of 30000 random episodes, and evaluated on an additional 1000 test episodes. We used to produce these plots, but found that the result was consistent over different shot counts.