Multi-Agent Routing Value Iteration Network
Abstract
In this paper we tackle the problem of routing multiple agents in a coordinated manner. This is a complex problem that has a wide range of applications in fleet management to achieve a common goal, such as mapping from a swarm of robots and ride sharing. Traditional methods are typically not designed for realistic environments which contain sparsely connected graphs and unknown traffic, and are often too slow in runtime to be practical. In contrast, we propose a graph neural network based model that is able to perform multi-agent routing based on learned value iteration in a sparsely connected graph with dynamically changing traffic conditions. Moreover, our learned communication module enables the agents to coordinate online and adapt to changes more effectively. We created a simulated environment to mimic realistic mapping performed by autonomous vehicles with unknown minimum edge coverage and traffic conditions; Our approach significantly outperforms traditional solvers both in terms of total cost and runtime. We also show that our model trained with only two agents on graphs with a maximum of 25 nodes can easily generalize to situations with more agents and/or nodes.
1 Introduction
As robots become ubiquitous, one of the fundamental problems is to be able to route a fleet or swarm of robots to perform a task. Several approaches have been developed to try to solve this task. The traveling salesman problem (TSP) is a classic NP-Hard (Toth and Vigo, 2002) problem in computer science, wherein an agent must visit a set of points while traveling the shortest possible distance. The natural multi-agent generalization of this problem is known as the vehicle routing problem (VRP) (Toth and Vigo, 2002), where multiple agents work in tandem to ensure that all points are visited exactly once. Despite a plethora of classic approaches to these problems (Applegate et al., 2006; Helsgaun, 2017), solvers are typically structured for offline planning and generally are unable to adapt their solutions online. Furthermore, these solvers do not incorporate online communication between the agents which is very desirable in many practical settings. These are not necessarily weaknesses of the solutions but rather the oversimplification of the problem definition itself.
Recently proposed deep learning methods have presented promising results in approximating solutions with much faster runtime (Vinyals et al., 2015; Khalil et al., 2017; Kool et al., 2019; Deudon et al., 2018). However, they are often tested on simplistic planar graph benchmarks with limited exploration on multi-agent settings. Moreover, none of these methods were designed towards dynamic environments where online communication can be very beneficial.
We focus on the realistic multi-agent autonomous mapping problem: given a fleet of vehicles, find the minimum total cost to map an urban region subject to traffic conditions, such that each road in the city is traversed at least a certain number of times, where the number is unknown a priori. This is a realistic setting for autonomous mapping as a region might need to be recollected due to occlusions, heavy traffic, bad localization, sensor failure, bad weather conditions, etc. Unfortunately neither VRP solutions nor existing deep learning methods perform well in this difficult scenario.
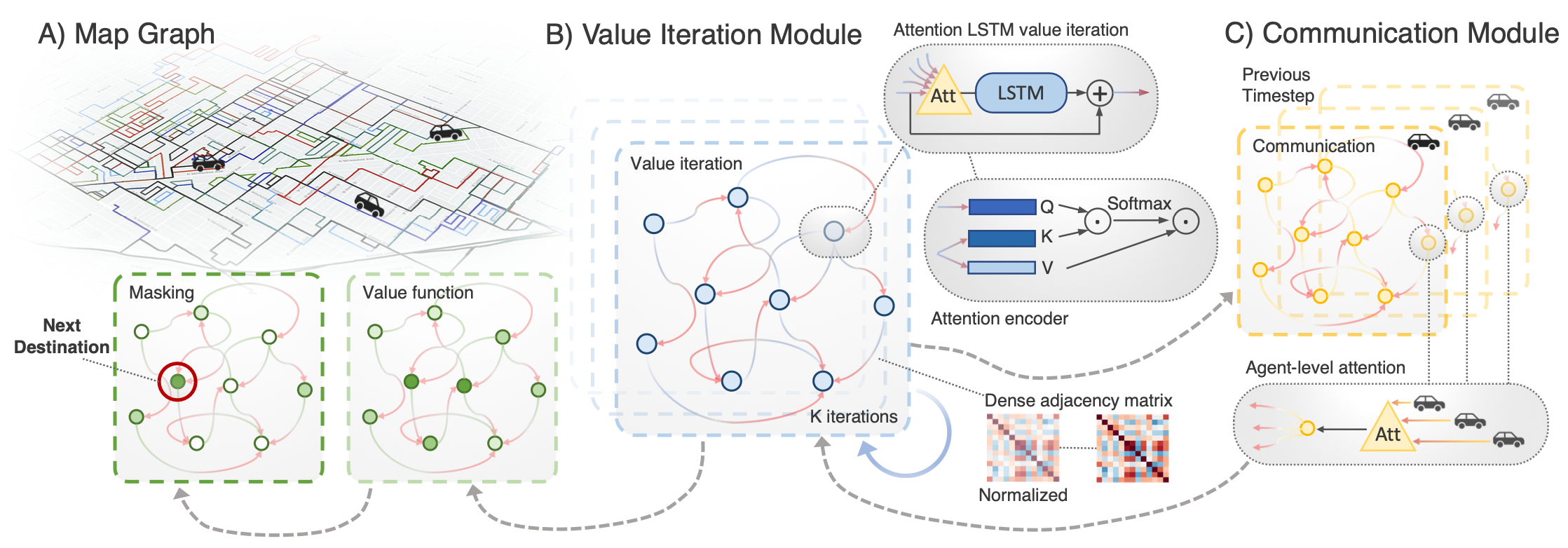
In this paper we propose the Multi Agent Routing Value Iteration Network (MARVIN), a distributed deep neural net tasked with the coordination of a swarm of vehicles to achieve a specific goal. In particular, each agent performs local planning in a learned value iteration module which exploits inter-agent communication through a novel learned communication protocol using the an attention mechanism. As we focus on sparse road graphs, our second contribution is the use of a dense adjacency matrix that encodes pairwise edge information to speed up information exchange and enable more rich node encodings.
We demonstrate the effectiveness of our approach on real road maps extracted from 18 different cities from around the world, using realistic traffic flow simulation (Tampère et al., 2011; Sewall et al., 2010). To create our training and evaluation examples containing the aforementioned realistic mapping challenges, we randomly subsample subgraphs on those cities, for each node in each graph we then randomly sample the number of times it has to be covered. Note that this information will be unknown to the fleet, and will only discovered upon reaching this number. We exploit total traversal time as our primary evaluation metric, and show that our approach achieves better performance than state-of-the-art conventional VRP solvers (Helsgaun, 2017), as well as recently proposed deep learning models (Kool et al., 2019; Deudon et al., 2018; Niu et al., 2018). Furthermore, MARVIN generalizing well to the graph size and the number of agents guaranteeing a full graph completion.
2 Related Work
In this section, we discuss previous attempts to solve vehicle routing problems. Background on graph neural networks and value iteration networks is also provided.
Vehicle routing problem:
Existing VRP solvers can be broken down into two categories: conventional iterative solvers and deep learning methods. Conventional solvers are usually iterative and designed to eventually converge to the true optimal of the system (Applegate et al., 2006; Fischetti et al., 2003; Helsgaun, 2017). Some solvers are only designed towards 2D planar graphs (Erdogan, 2017; Bae et al., 2007; Montero et al., 2017). Structured for offline planning, they are generally unable to adapt their solutions online. Moreover, they are not capable of any online communication between agents to incorporate local observations.
In contrast to conventional solvers, deep learning methods have recently emerged as efficient approximate solutions to combinatorial problems, thanks to the wide-spread success of attention mechanisms (Vinyals et al., 2015; Vaswani et al., 2017) and graph neural networks (Kipf and Welling, 2017; Khalil et al., 2017). Crucially, deep learning methods have powerful learning capabilities that can adapt easily to more complex and realistic problem definitions. While some simply try to improve subproblems of the VRP task (Zolfpour-Arokhlo et al., 2014; Barbucha, 2012; Kong et al., 2017), others produce end-to-end vehicle routes (Kool et al., 2019; Deudon et al., 2018). However, these deep learning solutions tend to assume that each node has a pair of 2D coordinates that can be used to identify its global position, and edges are connected using Euclidean distances, an unrealistic approximation of real road network graphs. Furthermore, PointerNet (Vinyals et al., 2015; Yu et al., 2019) and Encode-Attend-Navigate(EAN) (Deudon et al., 2018), two prominent deep learning TSP solvers, are restricted to the single agent domain, whereas (AM) (Kool et al., 2019), another deep learning solver which is able to operate in the multi-agent domain, only does so by creating a route for one agent after another, and thus is unable to control the exact number of agents being dispatched in each traversal. Moreover, none of these methods were designed to handle dynamic environments where one can benefit significantly from online communication.
Value iteration networks:
Deep learning based methods have also shown promising performance in path planning. One classical example is the value iteration network (Tamar et al., 2016), which embeds structural biases inspired from value iteration (Bellman, 1954) in a neural network. Gated path planning networks (Lee et al., 2018) changed the max-pooling layer with a generic long short-term memory (LSTM) (Hochreiter and Schmidhuber, 1997) significantly improving training stability which helps extend the number of iterations. These networks can naturally be translated to a graph domain by replacing the transitions with the edges in the graph, as is shown in the generalized value iteration network (GVIN) (Niu et al., 2018). However, they are developed to solve simple path planning environments such as 2D mazes and small graphs with weighted edges, and Dijkstra’s shortest path algorithm is already efficient and effective at solving these problems. Compared to the design of GVIN, our method features a dense adjacency matrix that is very effective at solving sparse graph coverage problems, where long range information exchange is needed.
Graph neural networks:
Graph neural networks (Scarselli et al., 2009; Wu et al., 2019) provide a way to learn graph representations that are both agnostic to the number of nodes in the graph and permutation invariant in the local neighborhood. Information from node neighborhood can be aggregated using graph convolutions (Kipf and Welling, 2017), recurrent neural networks (Li et al., 2016), and more recently via attention mechanisms (Yun et al., 2019; Velickovic et al., 2018). Graph attention modules also appear in deep learning based VRP/TSP solvers such as AM (Kool et al., 2019) and EAN (Deudon et al., 2018). Inspired by prior literature, we make use of graph attention in two ways: 1) a map-level road network augmented with graph attention within the planning module of each agent, and 2) an agent-level attention to aggregate messages received from other agents.
Multi-agent communication:
Traditional multi-agent communication in robotics has focused on heuristic and algorithmic approaches to improve communication efficiency (Pavone, 2010; Arkin et al., 1993; Berna-Koes et al., 2004). In contrast, CommNet (Sukhbaatar et al., 2016) demonstrated that a swarm of agents can autonomously learn their own communication protocol. This has led to a focus on the nature of learned language protocols. Some studies (Sukhbaatar et al., 2016; Kobayashi et al., 2012; Jiang and Lu, 2018) propose ways to combine information among agents. Sukhbaatar et al. (2016) use a simple summation across the messages, whereas Jiang and Lu (2018) leverage the attention mechanism to identify useful information. Other works focus more on the difference between cooperative swarms, greedy individuals, and competing swarms with learned communication (McPartland et al., 2005; Tan, 1993). Finally, there is a large body of work on the scalability of robotic swarms (Khan et al., 2019), and the necessity of explicit communication to infer the actions of other agents (Gupta et al., 2017).
3 Problem Definition
In this section we first provide a precise definition of the multi-agent mapping problem. We then propose in the next section a decentralized deep neural network for coordinating a fleet of vehicles to solve this mapping problem. Formally, given a strongly connected directed graph representing the road connectivity, we would like to produce a routing path for a set of agents such that each vertex in is covered times in total across all agents. We consider the real-world setting where 1) is unknown to all agents until the number has been reached (i.e., only success/failure is revealed upon each action) and 2) only local traffic information can be observed.
We consider a decentralized setting, where each agent gathers local observations and information communicated from other agents, and outputs the route it needs to take in the next step. Here we assume that each agent can broadcast to the rest of the fleet as this is possible with today’s communication technology. We also constrain the policy of each agent to be the same, making the system more robust to failure.
Let be the routing action taken by agent at time , indicating the next node to traverse. We define a route as the sequence of actions , where each action represents an intermediate destination. We refer the reader to Table 1 for our notation.
The policy of a single agent can be formulated as a function of 1) the road network graph ; 2) local environment observation ; 3) the communication messages sent by other agents ; and 4) the state of the agent . Thus,
| (1) |
| Symbol | Description |
|---|---|
| Current timestep | |
| Map graph | |
| Number of agents | |
| Number of graph nodes | |
| Routing + communication policy | |
| Routing policy | |
| Time cost given a route | |
| Observation by agent at time | |
| State of agent at time | |
| Action taken by agent at time | |
| Message vector sent by agent at time | |
| Number of times node needs to be covered | |
| Agent ’s node features at -th value iteration | |
| The input communication features for agent i |
Assuming that a traffic model produces the time needed to traverse a route, we would like our multi-agent system to minimize the following objective:
| (2) | ||||
| subject to |
where is the number of times node is visited in a route .
4 Multi-Agent Routing Value Iteration Network
In this section, we describe our proposed approach to the multi-vehicle routing problem. Note that the model is running locally in each individual agent, as this makes it scale well with the number of agents and be more robust to failures. There are two main components of our approach. First, the communication module (Fig. 2C) works asynchronously to save messages sent from other agents in a temporary memory unit, and retrieves the content based on an attention mechanism at the agent level. Each time an agent needs to select a new destination, this information is then sent to the value iteration module for future planning. Second, the value iteration module (Fig. 2B) runs locally on each agent and iteratively estimates the value of traveling to each node in the road network graph for its next route (Figure 2A). Then an attention LSTM planning module iteratively refines the node features for a fixed number of iterations, and outputs the value function for each node. The node with the highest value will be considered as the next destination for the agent. We now describe the value iteration module followed by the communication module.
| Name | Dim. | Type |
|---|---|---|
| Sum of in/out edge weights | 2 | float |
| # of in/out edges | 2 | integer |
| Agent at | 1 | binary |
| is unexplored | 1 | binary |
| is fully covered | 1 | binary |
| Dist. from cur. pos. to | 1 | float |
| Traffic at | 1 | float |
| is adjacent | 1 | binary |
| Communication vector | 16 | float |
4.1 Value Iteration Module
Our model operates on a strongly connected graph representing the topology of the road network. As shown in Fig. 2, each street segment forms a node in the graph, and the goal for each agent is to pick a node to be its next destination. Given some initial node features, our approach refines them for a fixed number of iterations of the graph neural network, decodes the features into a scalar value function for each node, and then selects the node with the maximum value to be our next destination (see Fig. 2). We now provide more details on each of these steps.
Let be the set of initial node feature vectors with being the total number of nodes and let represent the input communication node features. We encode the node input features (see Table 2) through a linear layer to serve as initial features for the value iteration network:
| (3) |
At each planning iteration , we perform the following iterative update through an LSTM with an attention module across neighboring nodes:
| (4) |
for and is the total number of value iteration steps. is the hidden state of the LSTM, which contains one state vector per node, and is the adjacency matrix. As opposed to conventional methods where the binary adjacency matrix is used as the primary input to the network, we use the Floyd-Warshall algorithm to compute the dense distance matrix as an explicit input in our architecture, thereby ensuring more meaningful information can be utilized by our model. In particular, the matrix produced by the Floyd-Warshall algorithm encodes the pairwise minimum path distance between any pair of nodes, , which we normalize to form our dense adjacency matrix , where is the element-wise mean of , and is the element-wise standard deviation. As shown in our experiments, using our dense adjacency matrix results in significantly better planning than the binary connectivity matrix of GVIN (Niu et al., 2018)).
Graph attention layer:
Information exchange on the graph level happens in the attention module “” which is a transformer layer (Yun et al., 2019), that takes in the node features and the adjacency matrix, and outputs the transformed features. Specifically, we first compute the key, query, and value vectors for each node:
| (5) | ||||
| (6) | ||||
| (7) |
We then compute the attention between each node and every other node to create an attention matrix ,
| (8) |
We combine the graph adjacency matrix with the attention matrix to represent edge features as follows:
| (9) |
where is a learned multi-layer neural network.
The new node values are computed by combining the values produced by all other nodes according to the attention in the fused attention matrix. The output of the graph attention layer is then fed to an LSTM module:
| (10) |
This full process is repeated for a fix number of iterations before decoding.
Value masking and decoding:
After iterating the attention LSTM module for iterations, we use a linear layer to project the features into a scalar value function for each node on the graph. We mask out the value of all nodes that no longer need to be visited since they have been fully mapped, and take a softmax over all remaining nodes to get the action probabilities
| (11) |
Finally, we take the node that has the maximum probability value to be the next destination. The full route will be formed by connecting the current node and the destination by using a shortest path algorithm on the weighted graph. Note that the weights are intended to represent the expected time required to travel from one road segment to the next, and therefore are computed by dividing the length of the street segment by the average speed of the vehicles traversing it.
4.2 Communication Module
Due to the partial observation nature of our realistic problem setup (e.g., traffic and multiple revisits), it is beneficial to let the agents communicate their intended trajectories, thereby encouraging more collaborative behaviours. Towards this goal, our proposed model also features an attention-based communication module, where now attention is performed over the agents, not the street segments. Whenever an agent performs an action, it uses , the final encodings of the value iteration module, to output the communication vector : , which is then broadcasted to all agents. We express the communication vector as a set of node features in order to reflect the structure of the street graph environment. The most recent communication vector from each sender is temporarily saved on the receiver end. When an agent decides to take a new action, it applies an agent-level attention layer to aggregate information from its receiver inbox.
Let , be the messages that an agent receives from other agents concatenated together, where is the number of agents, is the number of nodes and is the features dimension. The agent transforms the communication vectors to produce a query and a value vector:
| (12) | ||||
| (13) |
The communication vector last outputted by this given agent is also called upon to produce a key vector:
| (14) |
This key vector is then similarly dotted with the query vectors from all other agents to form a learned linear combination of the communication vectors from all the other agents. We can then compute the aggregated communication as :
| (15) | ||||
| (16) |
will then be used as part of the node feature inputs to the value iteration module for the next step.
4.3 Learning
Our proposed network can be trained end-to-end using either imitation learning or reinforcement learning. Here we explore both possibilities. For imitation learning, we assume there is an oracle that can solve these planning problems. Note that this relies on a fully observable environment, and oftentimes the oracle solver will slow down the training process since we generate a training graph for each rollout. Alternatively, we also consider training the network using reinforcement learning, which is more difficult to train but directly optimizes the final objective. We now describe the learning algorithms in more details.
Imitation learning (IL):
To generate the ground-truth that we seek to imitate, we firstly provide an LKH3 solver with global information about each problem to solve as a fully observed environment. Based on the groundtruth past trajectory, each agent tries to predict the next move . We train the agent using “teacher-forcing” by minimizing the cross entropy loss for each action, summing across the rollout. In teacher forcing, the agents are forced to perform the same actions as the ground truth rollout at each timestep, and are penalized when their actions do not match that of their “teacher”. The loss is averaged across a mini-batch.
| (17) |
where denotes the probability of taking action given state .
Reinforcement learning (RL):
While imitation learning is effective, expert demonstration may not always be available for realistic environments. Instead, we can use reinforcement learning. We use REINFORCE (Williams, 1992) to train the network using episodic reinforcement learning, and set the negative total cost of the fully rolled out traversal to be the reward function, normalized across a mini-batch.
| (18) | ||||
| (19) |
5 Autonomous Mapping Benchmark
In this section we describe our novel autonomous mapping benchmark . The dataset contains 22,814 directed road graphs collected from 18 cities around the world from different continents. We refer the reader to Table 3 for statistics of our dataset. We use a separate city for testing purposes and 10% of the training set for validation. We also augment this benchmark with realistic traffic conditions and realistic mapping challenges. These extra challenges fall into the following categories: random revisits, realistic traffic and asynchronous execution.
Random revisits:
When mapping a road in the real world, it is possible that our initial mapping attempt could fail, due to occlusion, sensor uncertainty, etc. Therefore we would have to revisit that street an unknown number of times before it is fully mapped. In order to simulate this, at the beginning of each run, we assign each node in the street graph a hidden variable that corresponds to how many times it will have to be visited before it is fully mapped. During training, we sample this value uniformly from one to three. We also randomly sample this value uniformly from one to three during evaluation, except for when we specifically test for an alternate distribution (see Table 5).
Traffic simulation:
We also simulate unknown traffic congestion for each street. To find the equilibrium congestion at each node, we use the flow equations proposed in Tampère et al. (2011). This method simulates traffic as a flow problem wherein we wish to maximize the total movement of vehicles given a set of junction constraints. We use the number of incoming and outgoing lanes multiplied by the speed limit of those lanes to establish the flow constraints, and initialize the congestion randomly using a uniform distribution from 0 to 1. Once we find an approximation for the equilibrium congestion, following Sewall et al. (2010) we define the velocity at each street to be: , where represents the speed limit of that road, is the traffic congestion on that road and is a hyperparameter (that we set to 3) that helps smooth out the effect of traffic. The effect of this is that whenever an agent travels to a particular node, the cost of performing this traversal is increased by . We cap this factor to a maximum value of 4 to ensure that the cost of traveling to nodes with maximum congestion does not extend to infinity. This allows the cost of an edge traversal to vary between 1 to 4 times its original value depending on the equilibrium congestion. Note that the congestion value of each node is unknown until the node is visited by an agent.
| Set | # Graphs | # Nodes |
|---|---|---|
| Train | 22,814 | 420,452 |
| Test | 373 | 14,284 |
Asynchronous execution:
During the training phase the agents act in a synchronous manner, where each agent is called sequentially to perform an action until the graph has been entirely mapped. This however does not take into account the time required to perform each action. During the evaluation phase, we instead simulate the time required to complete each action. Agents therefore act in an asynchronous way based on how long each action takes to complete.
6 Experiments
6.1 Implementation Details and Baselines
Each graph node has 16 communication channels for each agent. Similarly, the dimension of the encoding vectors is 16. For combining the dot-product attention with the distance matrix, a 3-layer [16-16-16] MLP with ReLU activation is used. When training, we set the learning rate of our model to be 1e-3 using the Adam optimizer, with a decay rate of 0.1 every 2000 epochs. We train our model for 5000 epochs. We use a batch size of 50 graphs, each of which has up to 25 nodes. We train our network with two agents only and evaluate with settings varying from one to nine agents.

| n = 25, 1 Agent | n = 25, 2 Agents | n = 50, 2 Agents | n = 100, 5 Agents | |||||||||
| Method | Cost | Gap | Runtime | Cost | Gap | Runtime | Cost | Gap | Runtime | Cost | Gap | Runtime |
| Oracle | 1.16 | 0.00% | 71.3 | 1.28 | 0.00% | 438 | 1.85 | 0.00% | 902 | 3.19 | 0.00% | 2430 |
| Random | 4.45 | 284.9% | 3.15 | 4.47 | 249.4% | 1.50 | 8.25 | 345.2% | 1.82 | 18.9 | 492.2% | 2.83 |
| Greedy | 2.12 | 73.7% | 3.37 | 2.33 | 81.8% | 2.11 | 3.55 | 91.5% | 3.57 | 10.4 | 227.0% | 22.3 |
| LKH3 | 1.26 | 8.84% | 71.2 | 1.80 | 40.5% | 438 | 2.54 | 37.3% | 902 | 6.14 | 92.5% | 2430 |
| GVIN | 1.37 | 18.8% | 52.5 | 1.48 | 15.9% | 44.2 | 2.45 | 32.1% | 63.4 | 5.41 | 69.6% | 48.6 |
| GAT | 1.53 | 32.5% | 43.0 | 1.56 | 21.6% | 29.1 | 2.58 | 39.7% | 38.0 | 5.43 | 70.2% | 38.2 |
| AM | 4.90 | 322.4% | 161 | - | - | - | - | - | - | - | - | - |
| EAN | 2.89 | 145.8% | 212 | - | - | - | - | - | - | - | - | - |
| MARVIN (IL) | 1.37 | 18.0% | 62.8 | 1.42 | 11.3% | 66.6 | 2.21 | 19.0% | 71.5 | 4.36 | 36.7% | 72.8 |
| MARVIN (RL) | 1.25 | 8.17% | 62.8 | 1.32 | 2.87% | 56.6 | 2.12 | 14.5% | 71.4 | 4.62 | 44.9% | 72.8 |
We compare our approach with the following baselines.
Random:
This baseline consists of visiting each node that has not been completely mapped yet in a random order.
Greedy:
Each agent visits the closest node that still needs to be mapped. It assumes that the agents are able to communicate which nodes have been fully mapped.
Lkh3:
represents the best performance of the iterative solver given limited information. We first allow the solver (Helsgaun, 2017) to calculate the optimal path for covering each node exactly once. Then, the solver calculates a new optimal path over all the remaining nodes that must be mapped. This is repeated until all nodes have been fully mapped. In essence, the solver performs VRP traversals until all nodes have been visited the desired number of times.
Gvin:
The Generalized Value Iteration Network (Niu et al., 2018) uses a GNN to propagate values on a graph. While the original implementation does not integrate communication between multiple agents, we enhanced GVIN with our attention communication module for fair comparison. This model was trained with imitation learning to achieve best performance.
Gat:
Graph Attention Networks (Velickovic et al., 2018) are similar to our method, in that they exchange information according to attention between two nodes in order to convey complex information. However, standard GAT architectures do not encode the distance matrix information and instead assume all edges have an equal weight, limiting their capabilities. While GATs are not necessarily designed to solve the TSP or VRP problems, they remain one of the state-of-the-art solutions for graph and network encoding.
Am:
The Attention Model (Kool et al., 2019) has been used as a deep learning VRP solver. Since it has no natural way to encode the information in the adjacency matrix, we add a Graph Convolution Network (GCN) encoding module at the beginning to perform this encoding and use imitation learning for training. The modification that the authors suggest for the AM algorithm to allow it to perform a VRP traversal does not allow for dynamic route adaptation, as is required in our environment. We therefore only evaluate this method in the single agent scenario.
Ean:
Encode-Attend-Navigate (Deudon et al., 2018) is a deep learning TSP solver designed very similarly to AM, but with a slightly different architecture. We enhance it with an additional GCN module at its beginning to encode the adjacency matrix in the same fashion as with AM. This model was trained with imitation learning as well.
Oracle:
This is the upper bound performance that an agent could have possibly achieved if given global information about all the hidden states. This solution is found by providing the LKH3 solver with details about all the hidden variables, and solving for the optimal plan. We transform the adjacency matrix by increasing the edge weights of the nodes effected by congestion, and by duplicating the nodes that will require multiple passes to be fully mapped.
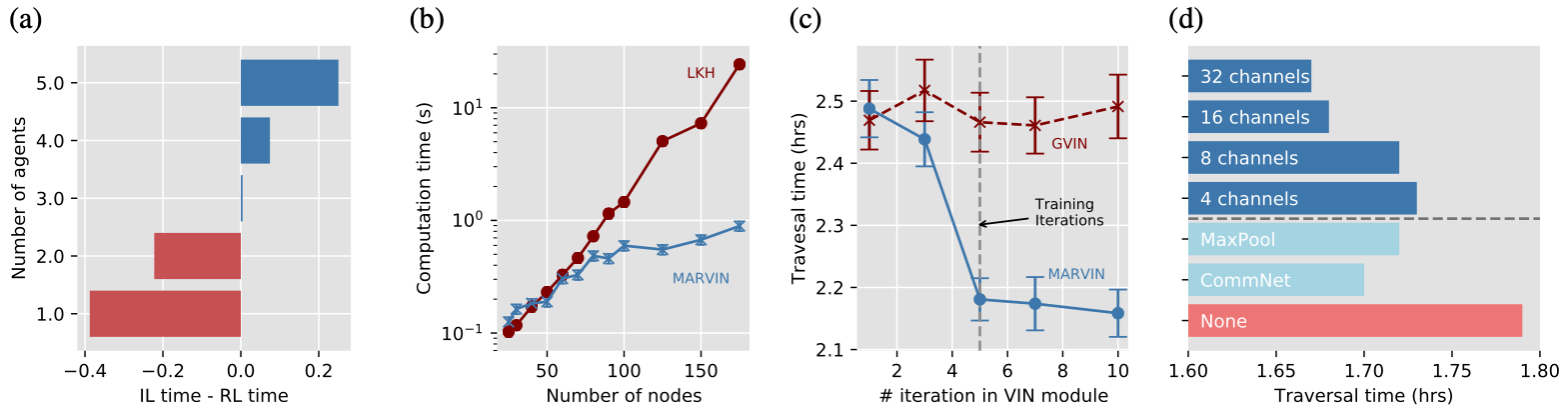
6.2 Results
Comparisons to Baselines:
As shown in Table 4, our method has the best performance across different numbers of agents and graph sizes. Notably, under 25 nodes and two agents, which is the training setting, our method with RL achieves a total cost that is within 3% from that of the oracle. We found our model trained with both reinforcement learning and imitation learning outperforms all competitor models. Overall, the model shows impressive generalization to more agents and larger graph size, since we limit the training of the model with two agents and 25 nodes. We also note that deep learning-based solvers that perform well in the more traditional TSP domain (AM, EAN) are unable to generalize well to our realistic benchmark. Specifically, the low performance of these deep learning solvers can be attributed to their inability to cope with mapping failures and nodes requiring multiple passes, which in turn is the result of their architecture not being structured for this problem formulation.
Load distribution:
The cost of performing each traversal is very evenly spread out amongs all of the agents. The maximum Gini coefficient for two agents observed on our evaluation set was 0.169, with the mean coefficient being around 0.075.
Scale to number of agents and graph size:
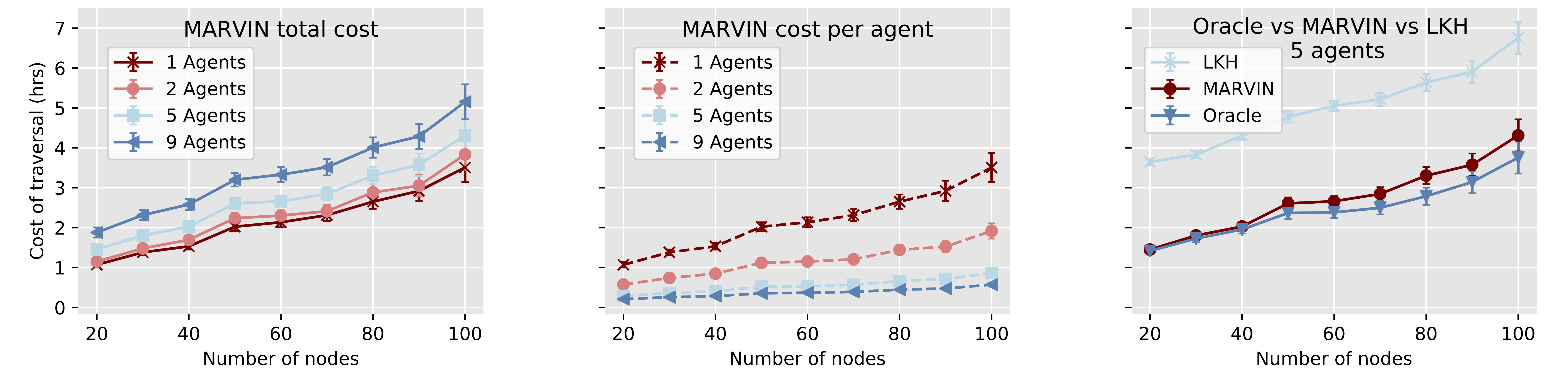
One of the primary focuses of our work is to develop a model that scales well with the number of agents and the size of the graph. Therefore, we evaluated our model’s performance on increasingly large graphs and observed how the performance varied with the number of agents. As shown in Fig. 3, the total cost increases marginally when we increase the total number of agents, indicating good scalability in this respect, and that our method performs much better than the current state of the art, as is represented by LKH.
We notice that models trained with RL appear to be able to generalize better when dealing with a larger number of agents, shown in Fig. 4A. This could be explained by the fact that supervised learning tries to exactly mimic the optimal strategy, which may not carry over when dealing with more agents, and therefore generalizes less effectively.
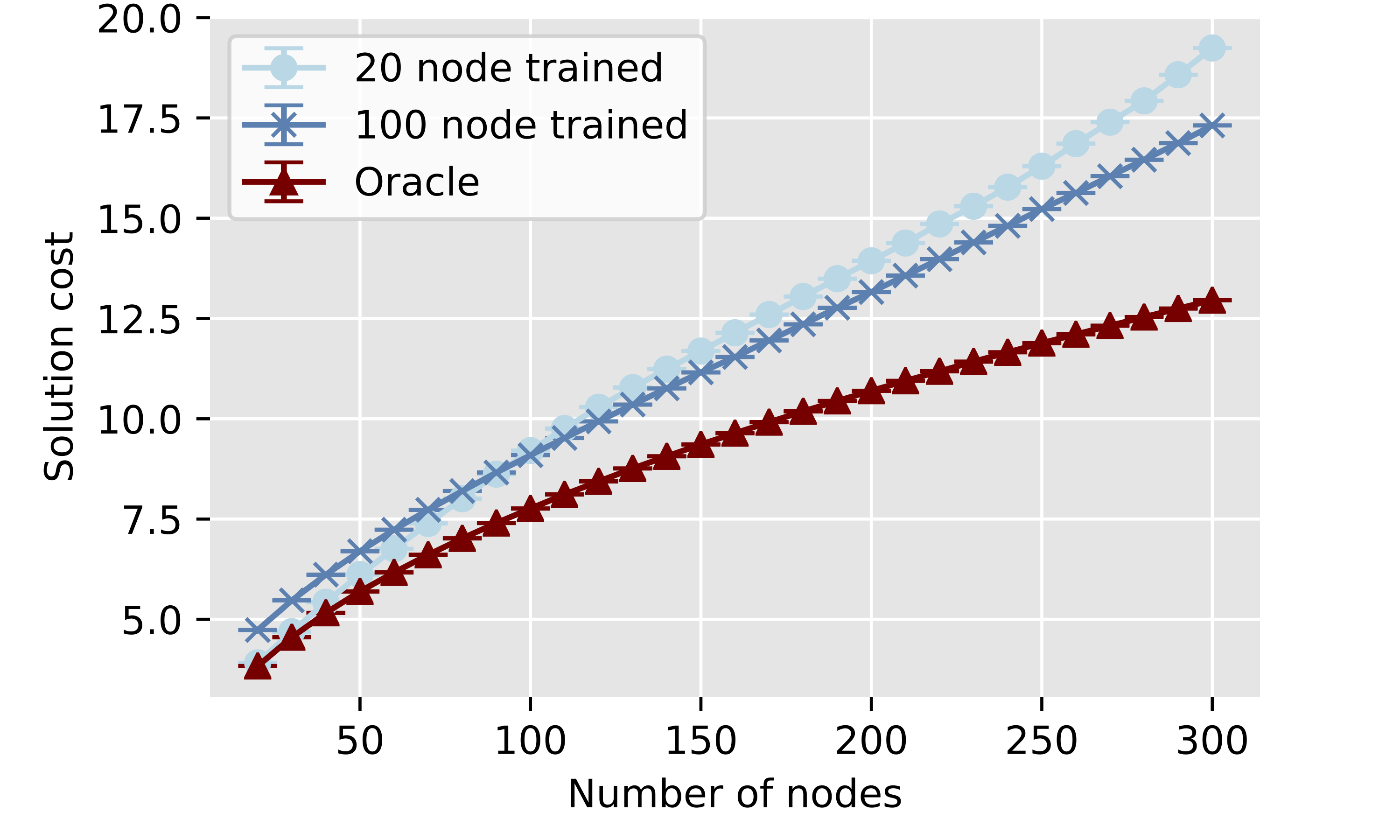
We also evaluate how a model trained on only toy graphs with 25 nodes compares with a graph trained only on toy graphs with 100 nodes. As shown in Fig. 5 ,the 100 node model scales much better on larger graphs, but that 25 node version of the model is able to perform much closer to true optimal when acting on smaller graphs.
Runtime:
An advantage that deep learning solutions have over conventional solvers is their runtime. We compare the average runtime of our model versus that of the LKH3 solver in Fig. 4B. Note that our model is significantly faster than LKH3 on large scale graphs with over 100 nodes.
Robustness to distribution shift:
We also evaluate the generalizability of our model to different “multiple pass” distributions. In order to simulate realistic mapping failures, each node must be revisited an unknown number of times before we say that it has been completely mapped. The “multiple pass” distributions is the distribution from which these numbers are selected. Shown in Table 5, our model has a consistent performance when we change the distribution at test time, despite being trained exclusively on the uniform 1-3 distribution.
| Multi-pass distribution | Oracle | LKH3 | Ours (RL) | Ours (IL) |
|---|---|---|---|---|
| Uniform 1 - 3 | 1.28 | 1.80 | 1.32 | 1.42 |
| Uniform 1 - 5 | 1.92 | 3.05 | 2.11 | 2.20 |
| Uniform 1 - 10 | 3.50 | 5.72 | 3.82 | 4.24 |
| TruncGaussian 1 - 3 | 1.51 | 2.52 | 1.75 | 1.79 |
| Either 2 or 4 | 1.72 | 2.49 | 1.84 | 2.01 |
| Only 3 | 1.52 | 1.92 | 1.68 | 1.68 |
| Exp (mean = 2) | 1.67 | 3.26 | 1.73 | 1.84 |
Number of value iterations:
In this experiment, we extend the number of iterations in our value iteration module to see if the module can benefit from longer reasoning. We originally trained our model with 5 iteration, and find that when we scale the number of iterations up to 10 during evaluation, the performance also further increases, as is seen in Fig. 4C.
| Method | Network Size | Cost | Gap | Runtime |
|---|---|---|---|---|
| Concorde (Oracle) | - | 4.22 | 0.00% | 40.1 |
| LKH3 | - | 4.22 | 0.00% | 159 |
| OR Tools | - | 4.27 | 1.11% | 15.0 |
| Random Insertion | - | 4.44 | 5.12% | 2.31 |
| Nearest Insertion | - | 4.84 | 14.7% | 15.4 |
| Farthest Insertion | - | 4.34 | 2.36% | 4.66 |
| Nearest Neighbour | - | 5.02 | 19.0% | 14.2 |
| AM (SS) | 28 MB | 4.24 | 0.51% | 16.3 |
| AM (SS + SP) | 28 MB | 4.23 | 0.13% | 552 |
| MARVIN | 0.04 MB | 4.54 | 7.56% | 61.7 |
| MARVIN (SS) | 0.04 MB | 4.32 | 2.38% | 18.9 |
| MARVIN (SS + SP) | 0.04 MB | 4.23 | 0.10% | 1714 |
Toy TSP:
To validate that our model can also solve toy TSP problems and thoroughly be compared with previous methods under their settings, we run a single-agent TSP benchmark with graphs of size 25 and uniformly generated vertices in a 1 by 1 square, following (Kool et al., 2019). Random, Nearest, and Farthest insertion, as well as nearest neighbour and AM are all taken from (Kool et al., 2019). Usually, in our problem setting the agent has no control over where it begins. However, since a complete TSP tour is independent of its starting position, we also test the effect of letting our model choose its starting position, which we denote as self-starting. We also evaluate how other conventional tour augmentation techniques affect our model’s performance. Sampling takes random samples from the action space of each of the agents and chooses the one with the lowest overall cost. When augmenting the method with trajectory sampling, we sample from 1280 model-guided stochastic runs. As shown in Table 6, we find that even though our model performs worse than the state-of-the-art attention model when we simply take a single greedy trajectory, it is able to outperform it when both models are augmented with trajectory sampling, getting within 0.10% of the optimal. It is also worth noting that our model is 800 times smaller than the best performer in terms of the number of parameters.
Visualization of large scale mapping:
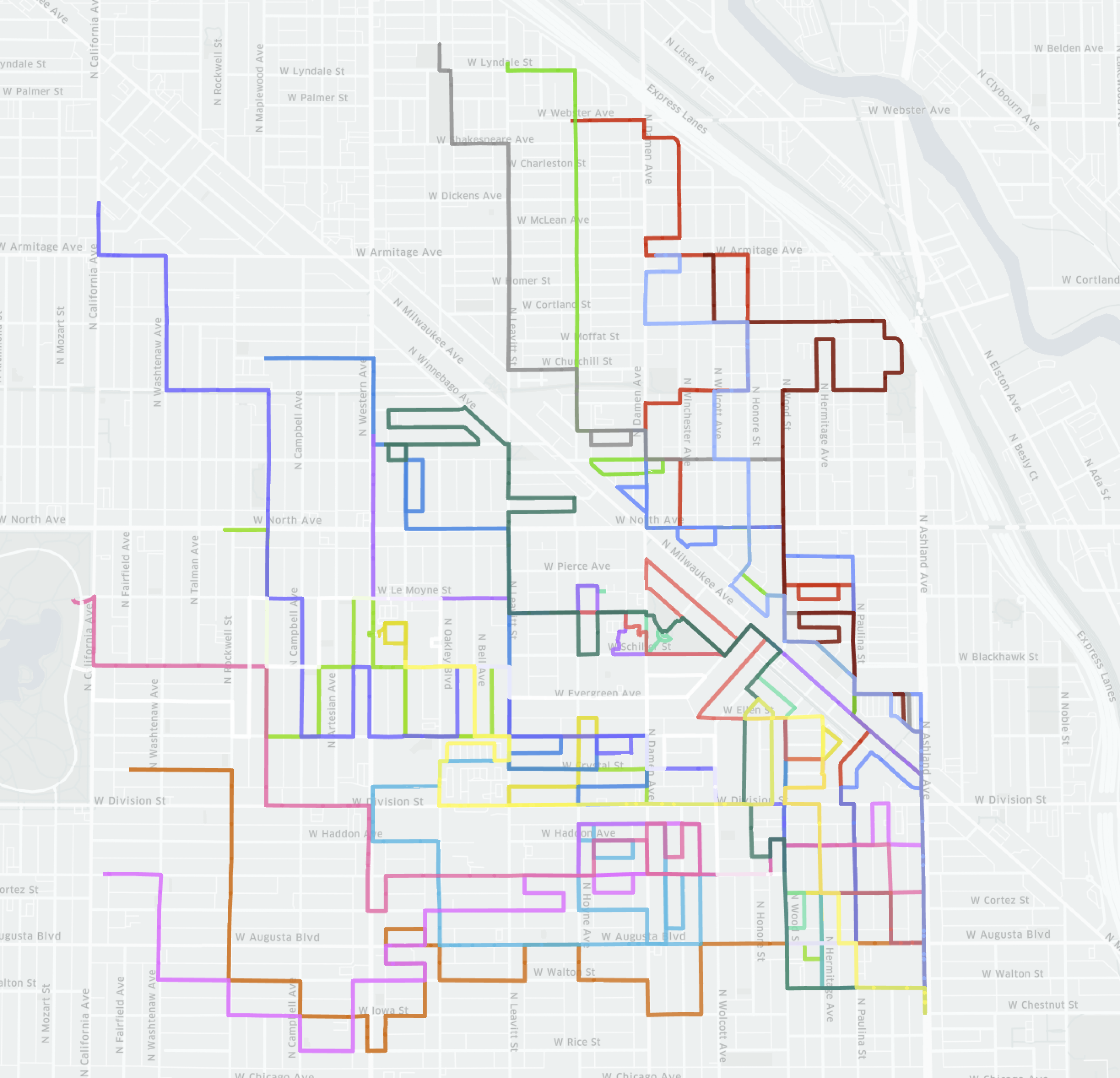
We also visualize our model navigating a swam of agents on a large portion of Chicago. Here we perform a large scale autonomous mapping simulation with a fleet of 20 vehicles on a graph of size 2426 nodes. We generally observe that when compared to other deep learning solutions, our model results in a much more thorough sweep, where it more rarely has to revisit previously seen regions. We further observe that models trained with imitation learning adopt more “exploratory” strategies, where agents split from the main swarm to visit new regions. For more details on the implications of this strategy please refer to the Appendix
| Variant | Attn. | Dense adj. | LSTM | Action Acc. |
|---|---|---|---|---|
| GVIN | 65.4% | |||
| GAT | ✓ | 23.5% | ||
| No LSTM | ✓ | ✓ | 71.7% | |
| Full | ✓ | ✓ | ✓ | 75.8% |
Value iteration module:
We investigated various design choices of the value iteration module, shown in Table 7, where we train different modules using IL and test them in terms of action prediction accuracy. As shown, GVIN, lacking the dense adjacency matrix and attention mechanism, is significantly worse than our model, and adding an LSTM further improves the performance by allowing an extended number of iterations of value reasoning.
Communication module:
We investigated different potential designs of the communication module, including CommNet style, MaxPooling, and the number of channels. As shown in Fig. 4D, we found that our attention based modules performs significantly better. Furthermore, the performance is improved with more channels.
7 Conclusion
In this paper we proposed a novel approach to perform online routing of a swarm of agents in the realistic domain where dynamic challenges are present. By making use of learned value iteration transitions and an attention based communication protocol, our model is able to outperform the state-of-the-art on real road graphs. Furthermore, it is able to do so in a scalable manner and can generalize well to different number of agents and nodes without re-training. Future work include performing a more in-depth analysis on the information encoded in the communication and its semantic meaning. There is also future exploration to be done into techniques to enable this system to run on massive graphs, as the memory usage during evaluation is still due to the pairwise adjacency matrix.
Acknowledgement
We thank Siva Manivasagam and Abbas Sadat for helpful discussions.
References
- Concorde tsp solver. Cited by: §1, §2.
- Communication of behavorial state in multi-agent retrieval tasks. In Proceedings IEEE International Conference on Robotics and Automation, ICRA, Cited by: §2.
- Integrated GA-VRP solver for multi-depot system. Computers & Industrial Engineering 53 (2), pp. 233–240. Cited by: §2.
- Search modes for the cooperative multi-agent system solving the vehicle routing problem. Neurocomputing 88, pp. 13–23. Cited by: §2.
- The theory of dynamic programming. Technical report Rand corp santa monica ca. Cited by: §2.
- Communication efficiency in multi-agent systems. In IEEE International Conference on Robotics and Automation, ICRA, Vol. 3. Cited by: §2.
- Learning heuristics for the TSP by policy gradient. In 15th International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, CPAIOR, Cited by: §1, §1, §2, §2, §6.1.
- An open source spreadsheet solver for vehicle routing problems. Computers & OR 84, pp. 62–72. Cited by: §2.
- Solving real-world atsp instances by branch-and-cut. In Combinatorial Optimization—Eureka, You Shrink!, pp. 64–77. Cited by: §2.
- Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems, AAMAS, pp. 66–83. Cited by: §2.
- An extension of the lin-kernighan-helsgaun tsp solver for constrained traveling salesman and vehicle routing problems. Roskilde: Roskilde University. Cited by: §1, §1, §2, §6.1.
- Long short-term memory. Neural computation 9 (8), pp. 1735–1780. Cited by: §2.
- Learning attentional communication for multi-agent cooperation. In Advances in Neural Information Processing Systems 31, NeurIPS, Cited by: §2.
- Learning combinatorial optimization algorithms over graphs. In Advances in Neural Information Processing Systems 30, NIPS, Cited by: §1, §2.
- Graph policy gradients for large scale robot control. CoRR abs/1907.03822. Cited by: §2.
- Semi-supervised classification with graph convolutional networks. In 5th International Conference on Learning Representations, ICLR, Cited by: §2, §2.
- Cooperative behavior acquisition in multi-agent reinforcement learning system using attention degree. In 19th International Conference on Neural Information Processing, ICONIP, Cited by: §2.
- Revisiting the master-slave architecture in multi-agent deep reinforcement learning. arXiv preprint arXiv:1712.07305. Cited by: §2.
- Attention, learn to solve routing problems!. In 7th International Conference on Learning Representations, ICLR, Cited by: §1, §1, §2, §2, §6.1, §6.2.
- Gated path planning networks. In Proceedings of the 35th International Conference on Machine Learning, ICML, pp. 2953–2961. Cited by: §2.
- Gated graph sequence neural networks. In 4th International Conference on Learning Representations, ICLR, Cited by: §2.
- Emergence of communication in competitive multi-agent systems: a pareto multi-objective approach. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, GECCO, Cited by: §2.
- An ilp-based local search procedure for the VRP with pickups and deliveries. Annals OR 259 (1-2), pp. 327–350. Cited by: §2.
- Generalized value iteration networks: life beyond lattices. In Proceedings of the Thirty-Second Conference on Artificial Intelligence, AAAI, Cited by: §1, §2, §4.1, §6.1.
- Dynamic vehicle routing for robotic networks. Ph.D. Thesis, Massachusetts Institute of Technology. Cited by: §2.
- The graph neural network model. IEEE Trans. Neural Networks 20 (1), pp. 61–80. Cited by: §2.
- Continuum traffic simulation. Comput. Graph. Forum 29 (2), pp. 439–448. Cited by: §1, §5.
- Learning multiagent communication with backpropagation. In Advances in Neural Information Processing Systems 29, NIPS, Cited by: §2.
- Value iteration networks. In Advances in Neural Information Processing Systems 29, NIPS, Cited by: §2.
- A generic class of first order node models for dynamic macroscopic simulation of traffic flows. Transportation Research Part B: Methodological 45 (1), pp. 289–309. Cited by: §1, §5.
- Multi-agent reinforcement learning: independent vs. cooperative agents. In Proceedings of the Tenth International Conference on Machine Learning, ICML, Cited by: §2.
- The vehicle routing problem. SIAM. Cited by: §1.
- Attention is all you need. In Advances in Neural Information Processing Systems 30, NIPS, Cited by: §2.
- Graph attention networks. In 6th International Conference on Learning Representations, ICLR, Cited by: §2, §6.1.
- Pointer networks. In Advances in Neural Information Processing Systems 28, NIPS, Cited by: §1, §2.
- Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning 8 (3), pp. 229–256. External Links: ISSN 1573-0565, Document Cited by: §4.3.
- A comprehensive survey on graph neural networks. CoRR abs/1901.00596. External Links: 1901.00596 Cited by: §2.
- Online vehicle routing with neural combinatorial optimization and deep reinforcement learning. IEEE Trans. Intelligent Transportation Systems 20 (10), pp. 3806–3817. Cited by: §2.
- Graph transformer networks. In Advances in Neural Information Processing Systems 32, NeurIPS, Cited by: §2, §4.1.
- Modeling of route planning system based on q value-based dynamic programming with multi-agent reinforcement learning algorithms. Engineering Applications of Artificial Intelligence 29, pp. 163–177. Cited by: §2.
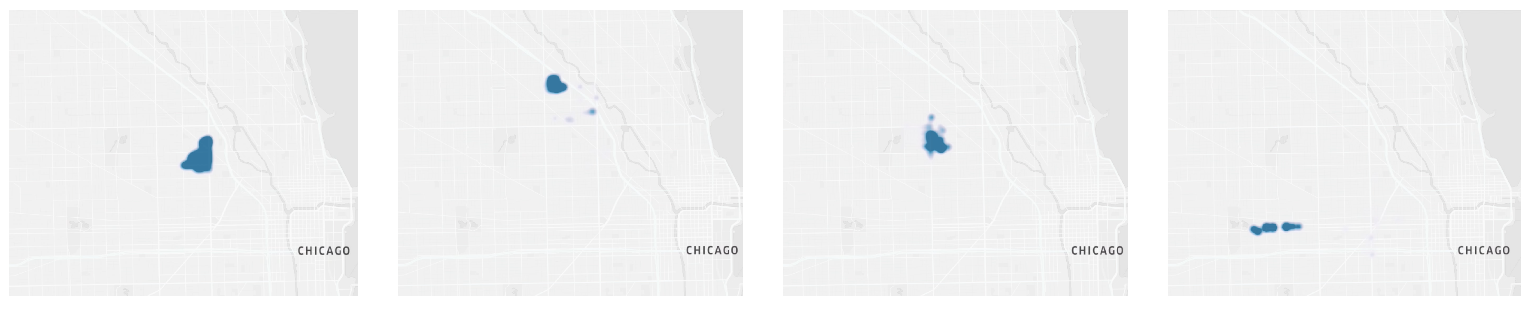
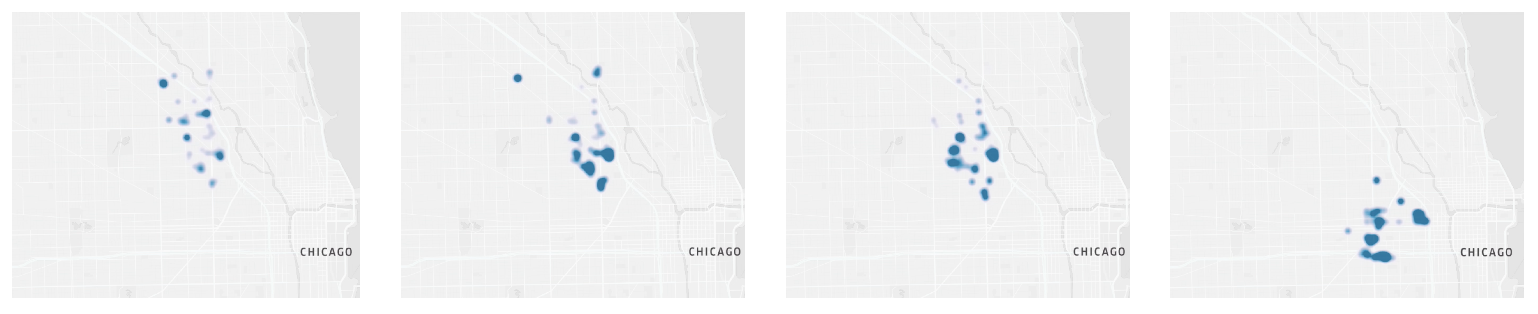
Appendix A Model Action Visualization
We firstly perform a qualitative analysis as to what kind of decisions each agent makes, and what these decisions look like at the value function level. We then we visualize the paths that a fleet of agents takes when mapping a large portion of Chicago from a bird’s-eye-view perspective. We use this to again qualitatively compare the strategies exploited by MARVIN trained with RL, MARVIN trained with IL, and the GVIN.
a.1 Value Function Heat Map
Upon performing an analysis of the value function, we find that two main behaviors are observed. The first is that the agent localizes the highest points in its value function to a small region of unvisited streets. This is equivalent to having this small cluster assigned to the agent by the collective swarm, and then it sequentially visiting all the streets until they recieve a new objective or finish with this cluster, as can be see in Figure 6.
The secondary observed behavior, as seen in Figure 7, is that the agents occasionally begin increasing their value function at far away nodes. This can be interpreted as the exploration phase, where the agents are encouraged to travel longer distances in order to reach new subclusters that need to be mapped. The peaks of the value function also appear to be relatively sporadic, indicating the ability of the agents to consider a wide variety of potential routes.
a.2 Overall Swarm Strategy
We qualitatively compare our model’s overall strategy to that of the generalized value iteration network (GVIN) and observe that in general, the GVIN network tends to promote exploration. We also observe that this high level strategy fails to cover all streets in a reliable manner. There are small sections throughout the graph that remain unvisited, and in order to perform a full traversal the agents must eventually return to these small unvisited sections, often covering significant distances in the process. This stands in contrast to what we observe with MARVIN, where the network prioritizes covering each street in a region before moving on to the next area. This ultimately results in less of a need for revisited regions that have incomplete mapping.
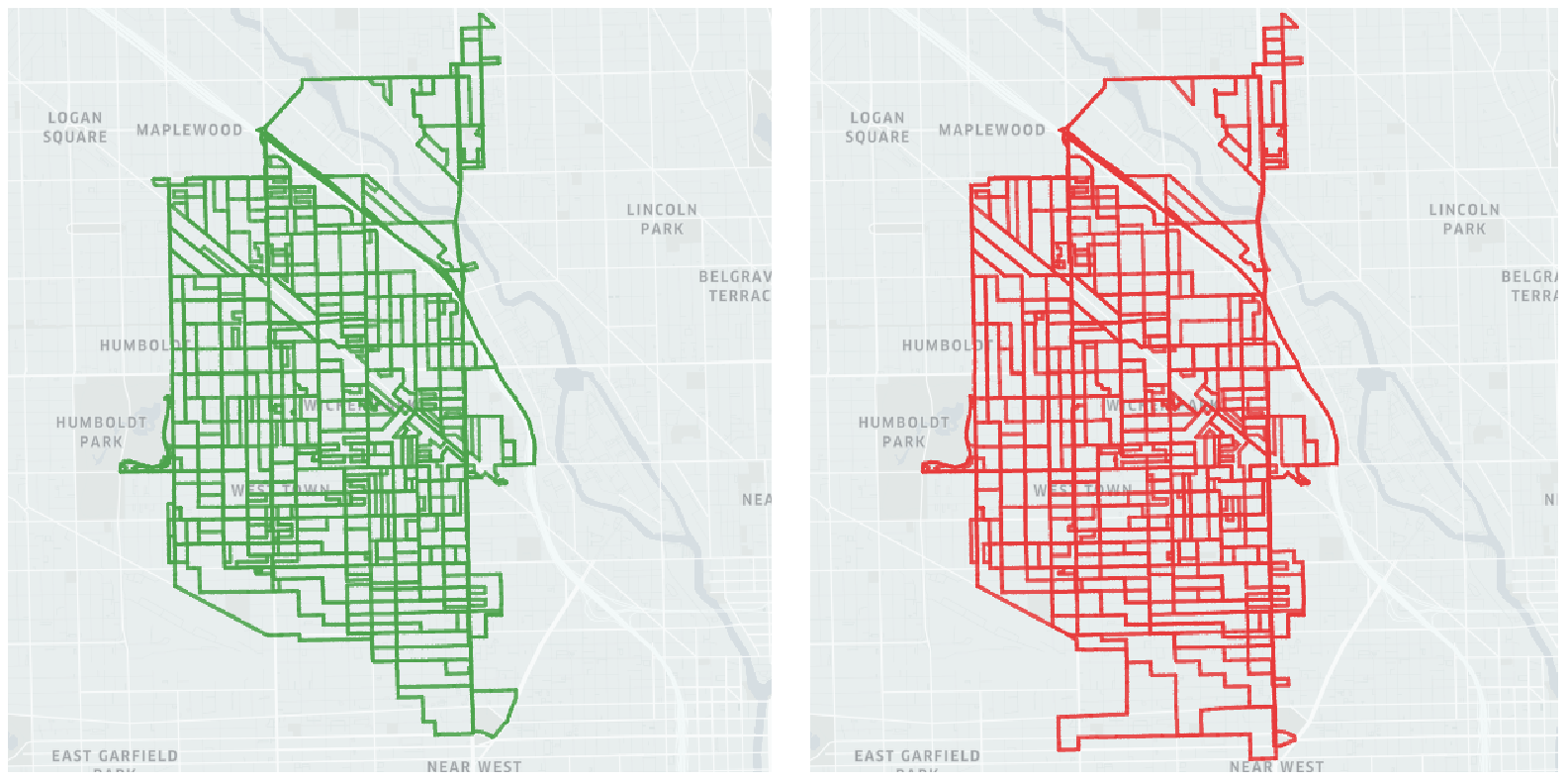
Next, we compare the high level strategy of MARVIN when trained with reinforcement learning to that when trained with imitation learning. We observe that in this context, both methods prioritize a thorough traversal, but that the agents trained using imitation learning are more efficient and therefore are able to expand to new regions much quicker than the agents trained with reinforcement learning. This matches the trend we noted when comparing training procedures and the scalability of the models that they produce.
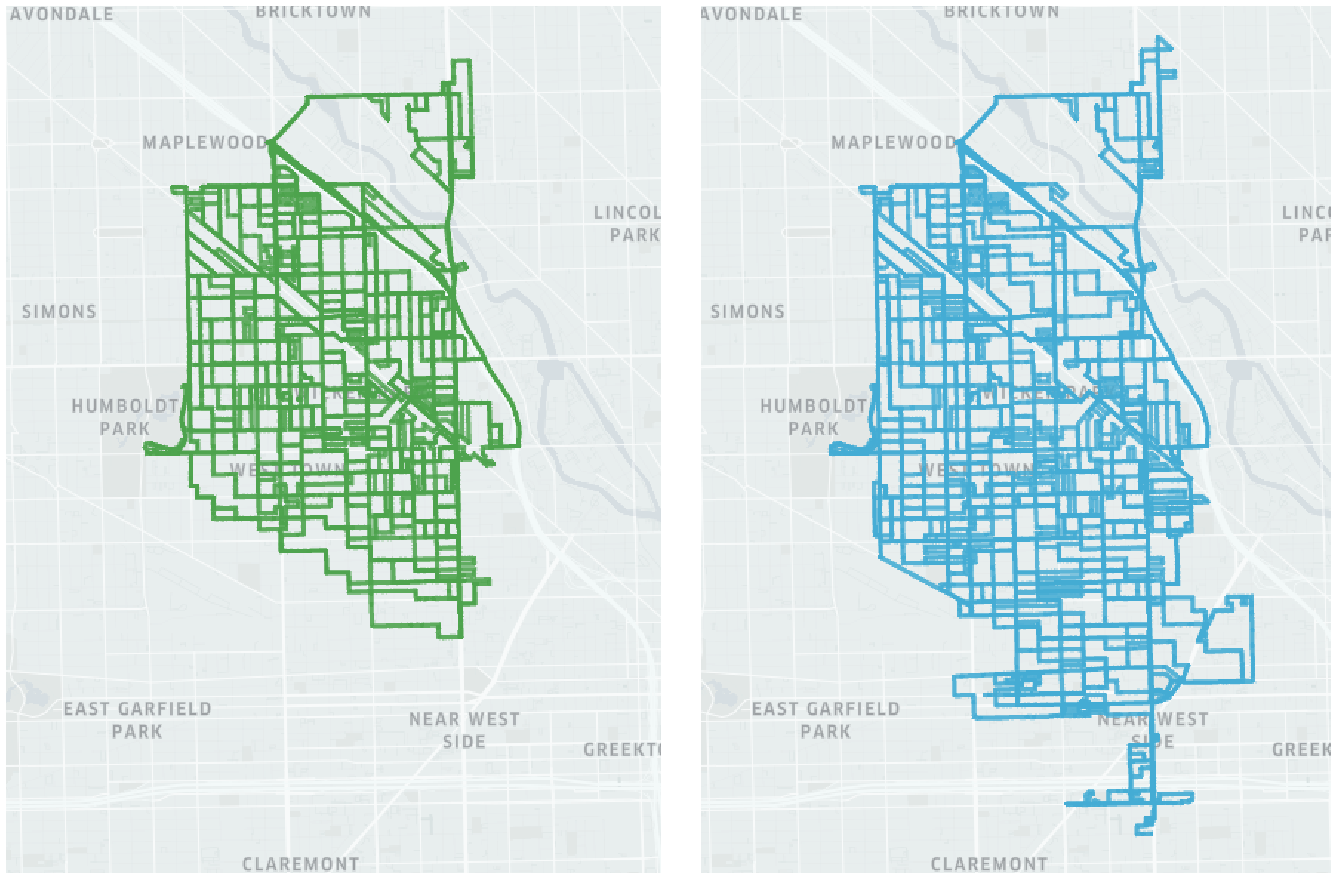
Appendix B Sample Graph Visualization
We visualize a few of the graphs that are used in the training process seen in Figure 10. While each one can be represented by a strongly connected graph, they nevertheless posess distinct features which enable a higher degree of generalization during the training process.