Graph HyperNetworks for
Neural Architecture Search
Abstract
Neural architecture search (NAS) automatically finds the best task-specific neural network topology, outperforming many manual architecture designs. However, it can be prohibitively expensive as the search requires training thousands of different networks, while each can last for hours. In this work, we propose the Graph HyperNetwork (GHN) to amortize the search cost: given an architecture, it directly generates the weights by running inference on a graph neural network. GHNs model the topology of an architecture and therefore can predict network performance more accurately than regular hypernetworks and premature early stopping. To perform NAS, we randomly sample architectures and use the validation accuracy of networks with GHN generated weights as the surrogate search signal. GHNs are fast – they can search nearly 10 faster than other random search methods on CIFAR-10 and ImageNet. GHNs can be further extended to the anytime prediction setting, where they have found networks with better speed-accuracy tradeoff than the state-of-the-art manual designs.
1 Introduction
The success of deep learning marks the transition from manual feature engineering to automated feature learning. However, designing effective neural network architectures requires expert domain knowledge and repetitive trial and error. Recently, there has been a surge of interest in neural architecture search (NAS), where neural network architectures are automatically optimized.
One approach for architecture search is to consider it as a nested optimization problem, where the inner loop finds the optimal parameters for a given architecture w.r.t. the training loss , and the outer loop searches the optimal architecture w.r.t. a validation loss :
| (1) |
| (2) |
Traditional NAS is expensive since solving the inner optimization in Eq. 1 requires a lengthy optimization process (e.g. stochastic gradient descent (SGD)). Instead, we propose to learn a parametric function approximation referred to as a hypernetwork (Ha et al., 2017; Brock et al., 2018), which attempts to generate the network weights directly. Learning a hypernetwork is an amortization of the cost of solving Eq. 1 repeatedly for multiple architectures. A trained hypernetwork is well correlated with SGD and can act as a much faster substitute.
Yet, the architecture of the hypernet itself is still to be determined. Existing methods have explored a variety of tactics to represent architectures, such as an ingenious 3D tensor encoding scheme (Brock et al., 2018), or a string serialization processed by an LSTM (Zoph and Le, 2017; Zoph et al., 2018; Pham et al., 2018). In this work, we advocate for a computation graph representation as it allows for the topology of an architecture to be explicitly modeled. Furthermore, it is intuitive to understand and can be easily extensible to various graph sizes.
To this end, in this paper we propose the Graph HyperNetwork (GHN), which can aggregate graph level information by directly learning on the graph representation. Using a hypernetwork to guide architecture search, our approach requires significantly less computation when compared to state-of-the-art methods. The computation graph representation allows GHNs to be the first hypernetwork to generate all the weights of arbitrary CNN networks rather than a subset (e.g. Brock et al. (2018)), achieving stronger correlation and thus making the search more efficient and accurate.
While the validation accuracy is often the primary goal in architecture search, networks must also be resource aware in real-world applications. Towards this goal, we exploit the flexibility of the GHN by extending it to the problem of anytime prediction. Models capable of anytime prediction progressively update their predictions, allowing for a prediction at any time. This is desirable in settings such as real-time systems, where the computational budget available for each test case may vary greatly and cannot be known ahead of time. Although anytime models have non-trivial differences to classical models, we show the GHN is amenable to these changes.
We summarize our main contributions of this work:
-
We propose Graph HyperNetwork that predicts the parameters of unseen neural networks by directly operating on their computational graph representations.
-
Our approach achieves highly competitive results with state-of-the-art NAS methods on both CIFAR-10 and ImageNet-mobile and is 10 faster than other random search methods.
-
We demonstrate that our approach can be generalized and applied in the domain of anytime-prediction, previously unexplored by NAS programs, outperforming the existing manually designed state-of-the-art models.
2 Related Work
Various search methods such as reinforcement learning (Zoph and Le, 2017; Baker et al., 2017a; Zoph et al., 2018), evolutionary methods (Real et al., 2017; Miikkulainen et al., 2017; Xie and Yuille, 2017; Liu et al., 2018b; Real et al., 2018) and gradient-based methods (Liu et al., 2018c; Luo et al., 2018) have been proposed to address the outer optimization (Eq. 2) of NAS, where an agent learns to sample architectures that are more likely to achieve higher accuracy. Different from these methods, this paper places its focus on the inner-loop: inferring the parameters of a given network (Eq. 1). Following Brock et al. (2018); Bender et al. (2018), we opt for a simple random search algorithm to complete the outer loop.
While initial NAS methods simply train candidate architectures for a brief period with SGD to obtain the search signal, recent approaches have proposed alternatives in the interest of computational cost. Baker et al. (2017b) propose directly predicting performance from the learning curve, and Deng et al. (2017) propose to predict performance directly from the architecture without learning curve information. However, training a performance predictor requires a ground truth, thus the expensive process of computing the inner optimization is not avoided. Pham et al. (2018); Bender et al. (2018); Liu et al. (2018c) use parameter sharing, where a “one-shot” model containing all possible architectures in the search space is trained. Individual architectures are sampled by deactivating some nodes or edges in the one-shot model. In this case, predicting can be seen as using a selection function from the set of parameters in the one-shot model.
Prior work has shown the feasibility of predicting with a function approximator. Schmidhuber (1992, 1993) proposed “fast-weights”, where one network produces weight changes for another. HyperNetworks (Ha et al., 2017) generate the weights of another network and show strong results in large-scale language modeling and image classification experiments. SMASH (Brock et al., 2018) applied HyperNetworks to perform NAS, where an architecture is encoded as a 3D tensor using a memory channel scheme. In contrast, we encode a network as a computation graph and use a graph neural network. While SMASH predicts a subset of the weights, our graph model is able to predict all the free weights.
While earlier NAS methods focused on standard image classification and language modeling, recent literature has extended NAS to search for architectures that are computationally efficient (Tan et al., 2018; Dong et al., 2018; Hsu et al., 2018; Elsken et al., 2018; Zhou et al., 2018). In this work, we applied our GHN based search program on the task of anytime prediction, where we not only optimize for the final speed but the entire speed-accuracy trade-off curve.
3 Background
We review the two major building blocks of our model: graph neural networks and hypernetworks.
Graph Neural Network:
A graph neural network (Scarselli et al., 2009; Li et al., 2016; Kipf and Welling, 2017) is a collection of nodes and edges , where each node is a recurrent neural network (RNN) that individually sends and receives messages along the edges, spanning over the horizon of message passing. Each node stores an internal node embedding vector , and is updated recurrently:
| (3) |
where is a recurrent cell function and is the message received by at time step :
| (4) |
with the message function and the set of neighbors with incoming edges pointing towards . is often modeled with a long short-term memory (LSTM) unit (Hochreiter and Schmidhuber, 1997) or gated recurrent unit (GRU) (Cho et al., 2014), and with an MLP. Given a graph , we define the GNN operator to be a mapping from a set of initial node embeddings to a set of different node embeddings , parameterized by some learnable parameters :
| (5) |
Throughout propagation the node embeddings continuously aggregate graph level information, which can be used for tasks such as node prediction and graph prediction by further aggregation. Similar to RNNs, GNNs are typically learned using backpropagation through time (BPTT) (Werbos, 1990).
Hypernetwork:
A hypernetwork (Ha et al., 2017) is a neural network that generates the parameters of another network. For a typical deep feedforward network with layers, the parameters of the -th layer can be generated by a learned function :
| (6) |
where is the layer embedding, and is shared for all layers. The output dimensionality of the hypernetwork is fixed, but it’s possible to accommodate predicting weights for layers of varying kernel sizes by concatenating multiple kernels of the fixed size. Varying spatial sizes can also be accommodated by slicing in the spatial dimensions. Hypernetworks have been found effective in standard image recognition and text classification problems, and can be viewed as a relaxed weight sharing mechanism. Recently, they have shown to be effective in accelerating architecture search (Brock et al., 2018).
4 Graph Hypernetworks for Neural Architectural Search
Our proposed Graph HyperNetwork (GHN) is a composition of a graph neural network and a hypernetwork. It takes in a computation graph (CG) and generates all free parameters in the graph. During evaluation, the generated parameters are used to evaluate the fitness of a random architecture, and the top performer architecture on a separate validation set is then selected. This allows us to search over a large number of architectures at the cost of training a single GHN. We refer the reader to Figure 1 for a high level system overview.
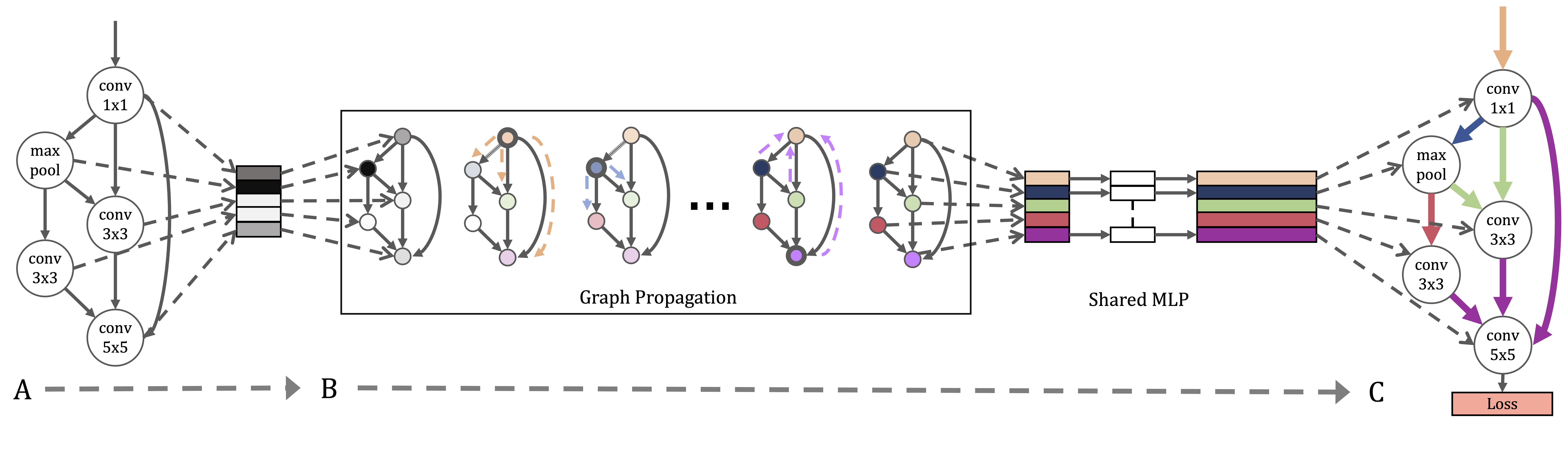
4.1 Graphical Representation
We represent a given architecture as a directed acyclic graph , where each node has an associated computational operator parametrized by , which produces an output activation tensor . Edges represent the flow of activation tensors from node to node . is computed by applying its associated computational operator on each of its inputs and taking summation as follows
| (7) |
4.2 Graph Hypernetwork
Our proposed Graph Hypernetwork is defined as a composition of a GNN and a hypernetwork. First, given an input architecture, we used the graphical representation discussed above to form a graph . A parallel GNN is then constructed to be homomorphic to with the exact same topology. Node embeddings are initialized to one-hot vectors representing the node’s computational operator. After graph message-passing steps, a hypernet uses the node embeddings to generate each node’s associated parameters. Let be the embedding of node after steps of GNN propagation, and let be a hypernetwork parametrized by , the generated parameters are:
| (8) |
For simplicity, we implement with a multilayer perceptron (MLP). It is important to note that is shared across all nodes, which can be viewed as an output prediction branch in each node of the GNN. Thus the final set of generated weights of the entire architecture is found by applying on all the nodes and their respective embeddings which are computed by :
| (9) | ||||
| (10) | ||||
| (11) |
4.3 Architectural Motifs and Stacked GNNs
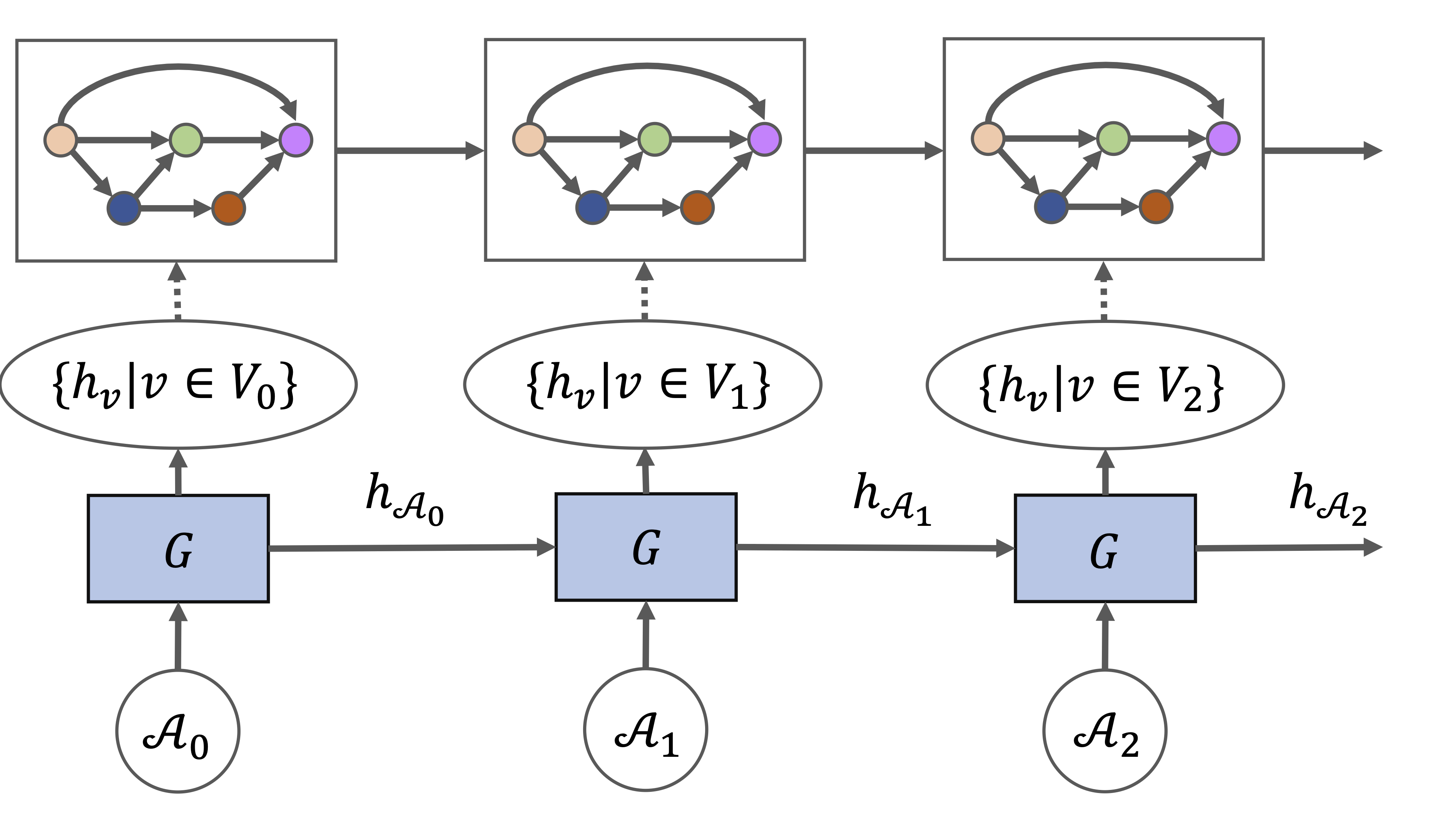
The computation graph of some popular CNN architectures often spans over hundreds of nodes (He et al., 2016a; Huang et al., 2017), which makes the search problem scale poorly. Repeated architecture motifs are originally exploited in those architectures where the computation of each computation block at different resolutions is the same, e.g. ResNet (He et al., 2016b). Recently, the use of architectural motifs also became popular in the context of neural architecture search, e.g. (Zoph et al., 2018; Pham et al., 2018), where a small graph module with a fewer number of computation nodes is searched, and the final architecture is formed by repeatedly stacking the same module. Zoph et al. (2018) showed that this leads to stronger performance due to a reduced search space; the module can also be transferred to larger datasets by adopting a different repeating pattern.
Our proposed method scales naturally with the design of repeated modules by stacking the same graph hypernetwork along the depth dimension. Let be a graph composed of a chain of repeated modules . A graph level embedding is computed by taking an average over all node embeddings after a full propagation of the current module, and passed onwards to the input node of the next module as a message before graph propagation continues to the next module.
| (12) | ||||
| (13) | ||||
| (14) |
Note that share parameters for all . Please see Figure 2 for an overview.
4.4 Forward-backward GNN message passing
Standard GNNs employ the synchronous propagation scheme (Li et al., 2016), where the node embeddings of all nodes are updated simultaneously at every step (see Equation 3). Recently, Liao et al. (2018) found that such propagation scheme is inefficient in passing long-range messages and suffers from the vanishing gradient problem as do regular RNNs. To mitigate these shortcomings they proposed asynchronous propagation using graph partitions. In our application domain, deep neural architectures are chain-like graphs with a long diameter; This can make synchronous message passing difficult. Inspired by the backpropagation algorithm, we propose another variant of asynchronous propagation scheme, which we called forward-backward propagation, that directly mimics the order of node execution in a backpropagation algorithm. Specifically, let be a topological sort of the nodes in the computation graph in a forward pass,
| (15) |
The total number of propagation steps for a full forward-backward pass will then become . Under the synchronous scheme, propagating information across a graph with diameter would require messages. This is reduced to under the forward-backward scheme.
4.5 Learning
Learning a graph hypernetwork is straightforward since are directly generated by a differentiable network. We compute gradients of the graph hypernetwork parameters using the chain rule:
| (16) |
The first term is the gradients of standard network parameters, the second term is decomposed as
| (17) | ||||
| (18) |
where (Eq. 17) is the contribution from GNN module and (Eq. 18) is the contribution from the hypernet module . Both and are jointly learned throughout training.
5 Experiments
In this section, we use our proposed GHN to search for the best CNN architecture for image classification. First, we evaluate the GHN on the standard CIFAR (Krizhevsky and Hinton, 2009) and ImageNet (Russakovsky et al., 2015) architecture search benchmarks. Next, we apply GHN on an “anytime prediction” task where we optimize the speed-accuracy tradeoff that is key for many real-time applications. Finally, we benchmark the GHN’s predicted-performance correlation and explore various factors in an ablation study.
5.1 NAS benchmarks
| Method | Search Cost (GPU days) | Param | Accuracy |
|---|---|---|---|
| SMASHv1 (Brock et al., 2018) | ? | 4.6 | 94.5 |
| SMASHv2 (Brock et al., 2018) | 3 | 16.0 | 96.0 |
| One-Shot Top (F=32) (Bender et al., 2018) | 4 | 2.7 0.3 | 95.5 0.1 |
| One-Shot Top (F=64) (Bender et al., 2018) | 4 | 10.4 1.0 | 95.9 0.2 |
| Random (F=32) | - | 4.6 0.6 | 94.6 0.3 |
| GHN Top (F=32) | 0.42 | 5.1 0.6 | 95.7 0.1 |
| Method | Search Cost (GPU days) | Param | Accuracy |
|---|---|---|---|
| NASNet-A (Zoph et al., 2018) | 1800 | 3.3 | 97.35 |
| ENAS Cell search (Pham et al., 2018) | 0.45 | 4.6 | 97.11 |
| DARTS (first order) (Liu et al., 2018c) | 1.5 | 2.9 | 97.06 |
| DARTS (second order) (Liu et al., 2018c) | 4 | 3.4 | 97.17 0.06 |
| GHN Top-Best, 1K (F=32) | 0.84 | 5.7 | 97.16 0.07 |
| Method | Search Cost (GPU days) | Param | Accuracy |
|---|---|---|---|
| NASNet-A (Zoph et al., 2018) | 1800 | 5.3 | 74.0 |
| NASNet-C (Zoph et al., 2018) | 1800 | 4.9 | 72.5 |
| AmoebaNet-A (Real et al., 2018) | 3150 | 5.1 | 74.5 |
| AmoebaNet-C (Real et al., 2018) | 3150 | 6.4 | 75.7 |
| PNAS (Liu et al., 2018a) | 225 | 5.1 | 74.2 |
| DARTS (second order) (Liu et al., 2018c) | 4 | 4.9 | 73.1 |
| GHN Top-Best, 1K | 0.84 | 6.1 | 73.0 |
5.1.1 Cifar-10
We conduct our initial set of experiments on CIFAR-10 (Krizhevsky and Hinton, 2009), which contains 10 object classes and 50,000 training images and 10,000 test images of size 32323. We use 5,000 images split from the training set as our validation set.
Search space:
Following existing NAS methods, we choose to search for optimal blocks rather than the entire network. Each block contains 17 nodes, with 8 possible operations. The final architecture is formed by stacking 18 blocks. The spatial size is halved and the number of channels is doubled after blocks 6 and 12. These settings are all chosen following recent NAS methods (Zoph and Le, 2017; Pham et al., 2018; Liu et al., 2018c), with details in the Appendix.
Training:
For the GNN module, we use a standard GRU cell (Cho et al., 2014) with hidden size 32 and 2 layer MLP with hidden size 32 as the recurrent cell function and message function respectively. The shared hypernetwork is a 2-layer MLP with hidden size 64. From the results of ablations studies in Section 5.4, the GHN is trained with blocks with nodes and propagations under the forward-backward scheme, using the ADAM optimizer (Kingma and Ba, 2015). Training details of the final selected architectures are chosen to follow existing works and can be found in the Appendix.
Evaluation:
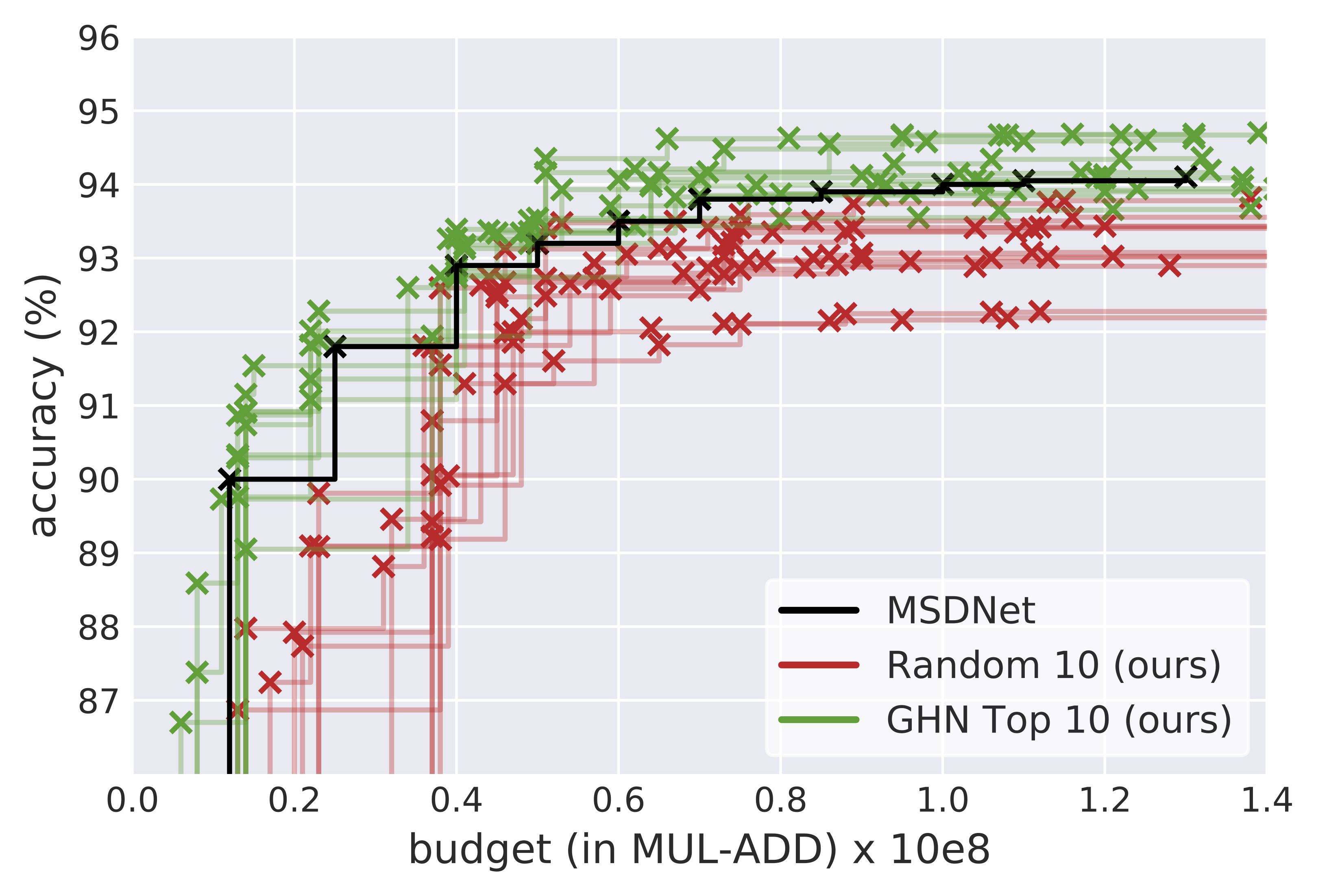
First, we compare to similar methods that use random search with a hypernetwork or a one-shot model as a surrogate search signal. We randomly sample 10 architectures and train until convergence for our random baseline. Next, we randomly sample 1000 architectures, and select the top 10 performing architectures with GHN generated weights, which we refer to as GHN Top. Our reported search cost includes both the GHN training and evaluation phase. Shown in Table 1, the GHN achieves competitive results with nearly an order of magnitude reduction in search cost.
In Table 2, we compare with methods which use more advanced search methods, such as reinforcement learning and evolution. Once again, we sample 1000 architectures and use the GHN to select the top 10. To make a fair comparison for random search, we train the top 10 for a short period before selecting the best to train until convergence. The accuracy reported for GHN Top-Best is the average of 5 runs of the same final architecture. Note that all methods in Table 2 use CutOut (Devries and Taylor, 2017). GHN achieves very competitive results with a simple random search algorithm, while only using a fraction of the total search cost. Using advanced search methods with GHNs may bring further gains.
5.1.2 ImageNet-Mobile
We also run our GHN algorithm on the ImageNet dataset (Russakovsky et al., 2015), which contains 1.28 million training images. We report the top-1 accuracy on the 50,000 validation images. Following existing literature, we conduct the ImageNet experiments in the mobile setting, where the model is constrained to be under 600M FLOPS. We directly transfer the best architecture block found in the CIFAR-10 experiments, using an initial convolution layer of stride 2 before stacking 14 blocks with scale reduction at blocks 1, 2, 6 and 10. The total number of flops is constrained by choosing the initial number of channels. We follow existing NAS methods on the training procedure of the final architecture; details can be found in the Appendix. As shown in Table 3 the transferred block is competitive with other NAS methods which require a far greater search cost.
5.2 Anytime Prediction
In the real-time setting, the computational budget available can vary for each test case and cannot be known ahead of time. This is formalized in anytime prediction, (Grubb and Bagnell, 2012) the setting in which for each test example , there is non-deterministic computational budget drawn from the joint distribution . The goal is then to minimize the expected loss , where is the model and is the loss for an that must produce a prediction within the budget .
We conduct experiments on CIFAR-10. Our anytime search space consists of networks with 3 cells containing 24, 16, and 8 nodes. Each node is given the additional properties: 1) the spatial size it operates at and 2) if an early-exit classifier is attached to it. A node enforces its spatial size by pooling or upsampling any input feature maps inputs that are of different scale. Note that while a naive one-shot model would triple its size to include three different parameter sets at three different scales, the GHN is negligibly affected by such a change. The GHN uses the area under the predicted accuracy-FLOPS curve as its selection criteria. The search space, contains various convolution and pooling operators. Training methodology of the final architectures are chosen to match Huang et al. (2018) and can be found in the Appendix.
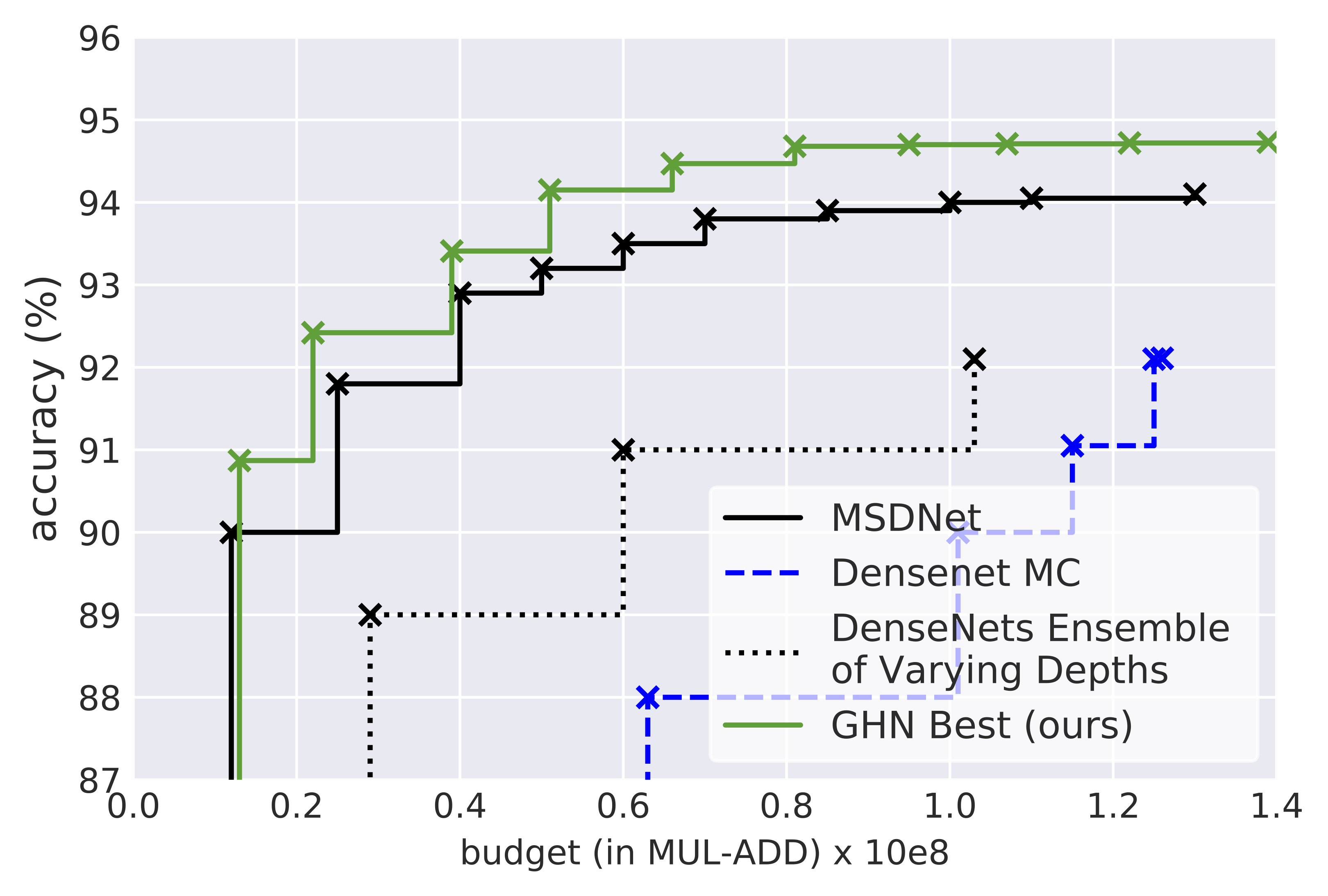
Figure 3 shows a comparison with the various methods presented by Huang et al. (2018). Our experiments show that the best searched architectures can outperform the current state-of-the-art human designed networks. We see the GHN is amenable to the changes proposed above, and can find efficient architectures with a random search when used with a strong search space.
5.3 Predicted performance correlation (CIFAR-10)
| Method | Computation cost | Correlation | ||
| Initial (GPU hours) | Per arch. (GPU seconds) | Random-100 | Top-50 | |
| SGD 10 Steps | - | 0.9 | 0.26 | -0.05 |
| SGD 100 Steps | - | 9 | 0.59 | 0.06 |
| SGD 200 Steps | - | 18 | 0.62 | 0.20 |
| SGD 1000 Steps | - | 90 | 0.77 | 0.26 |
| One-Shot | 9.8 | 0.06 | 0.58 | 0.31 |
| GHN | 6.1 | 0.08 | 0.68 | 0.48 |
In this section, we evaluate whether the parameters generated from GHN can be indicative of the final performance. Our metric is the correlation between the accuracy of a model with trained weights vs. GHN generated weights. We use a fixed set of 100 random architectures that have not been seen by the GHN during training, and we train them for 50 epochs to obtain our “ground-truth” accuracy, and finally compare with the accuracy obtained from GHN generated weights. We report the Pearson’s R score on all 100 random architectures and the top 50 performing architectures (i.e. above average architectures). Since we are interested in searching for the best architecture, obtaining a higher correlation on top performing architectures is more meaningful.
To evaluate the effectiveness of GHN, we further consider two baselines: 1) training a network with SGD from scratch for a varying number of steps, and 2) our own implementation of the one-shot model proposed by Pham et al. (2018), where nodes store a set of shared parameters for each possible operation. Unlike GHN, which is compatible with varying number of nodes, the one-shot model must be trained with nodes to match the evaluation. The GHN is trained with , using forward-backward propagation. These GHN parameters are selected based on the results found in Section 5.4.
Table 4 shows performance correlation and search cost of SGD, the one-shot model, and our GHN. Note that GHN clearly outperforms the one-shot model, showing the effectiveness of dynamically predicting parameters based on graph topology. While it takes 1000 SGD steps to surpasses GHN in the “Random-100” setting, GHN is still the strongest in the “Top-50” setting, which is more important for architecture search. Moreover, compared to GHN, running 1000 SGD steps for every random architecture is over 1000 times more computationally expensive. In contrast, GHN only requires a pre-training stage of 6 hours, and afterwards, the trained GHN can be used to efficiently evaluate a massive number of random architectures of different sizes.
5.4 Ablation Studies (CIFAR-10)
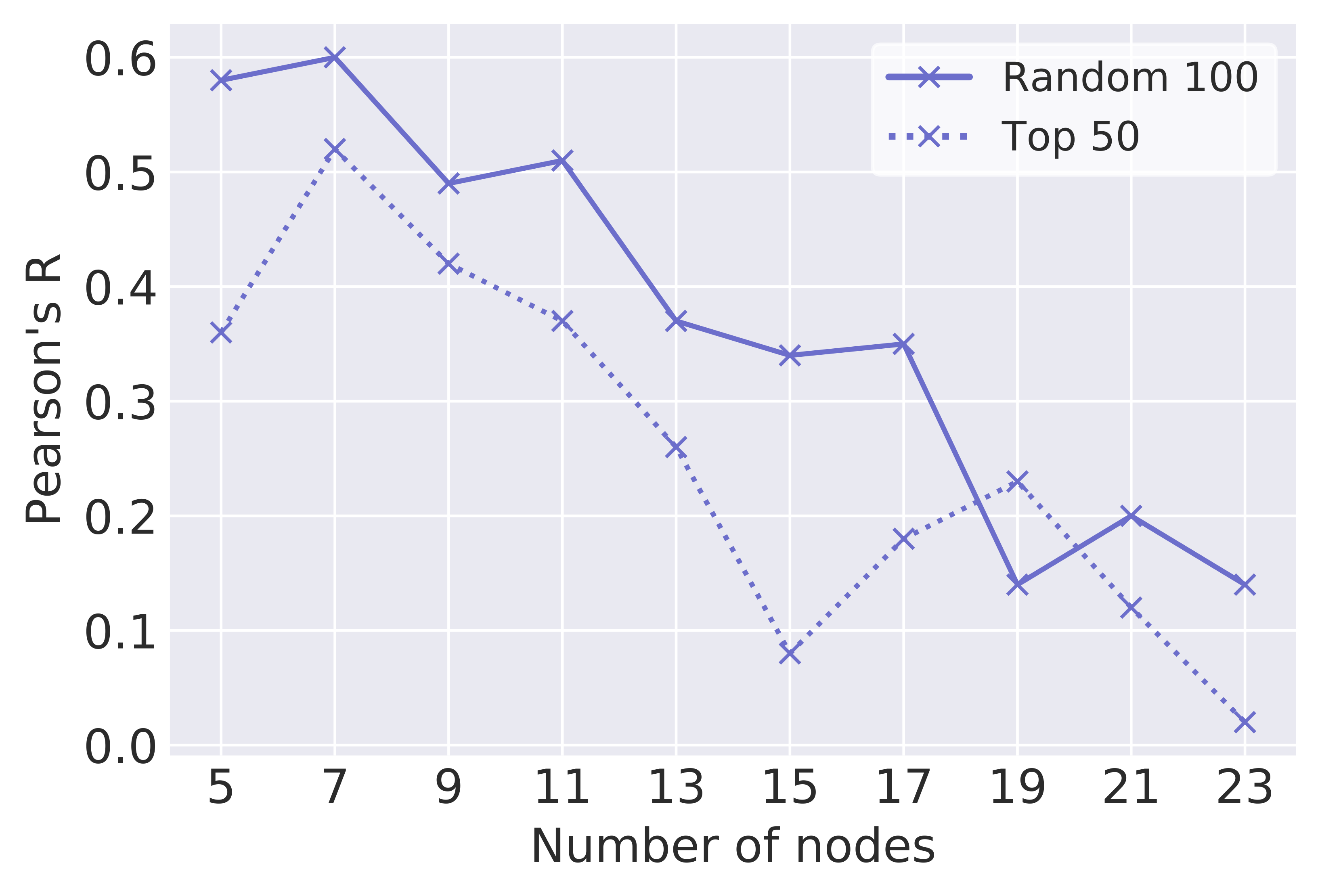
Number of graph nodes:
The GHN is compatible with varying number of nodes - graphs used in training need not be the same size as the graphs used for evaluation. Figure 5 shows how GHN performance varies as a function of the number of nodes employed during training - fewer nodes generally produces better performance. While the GHN has difficulty learning on larger graphs, likely due to the vanishing gradient problem, it can generalize well from just learning on smaller graphs. Note that all GHNs are tested with the full graph size ( nodes).
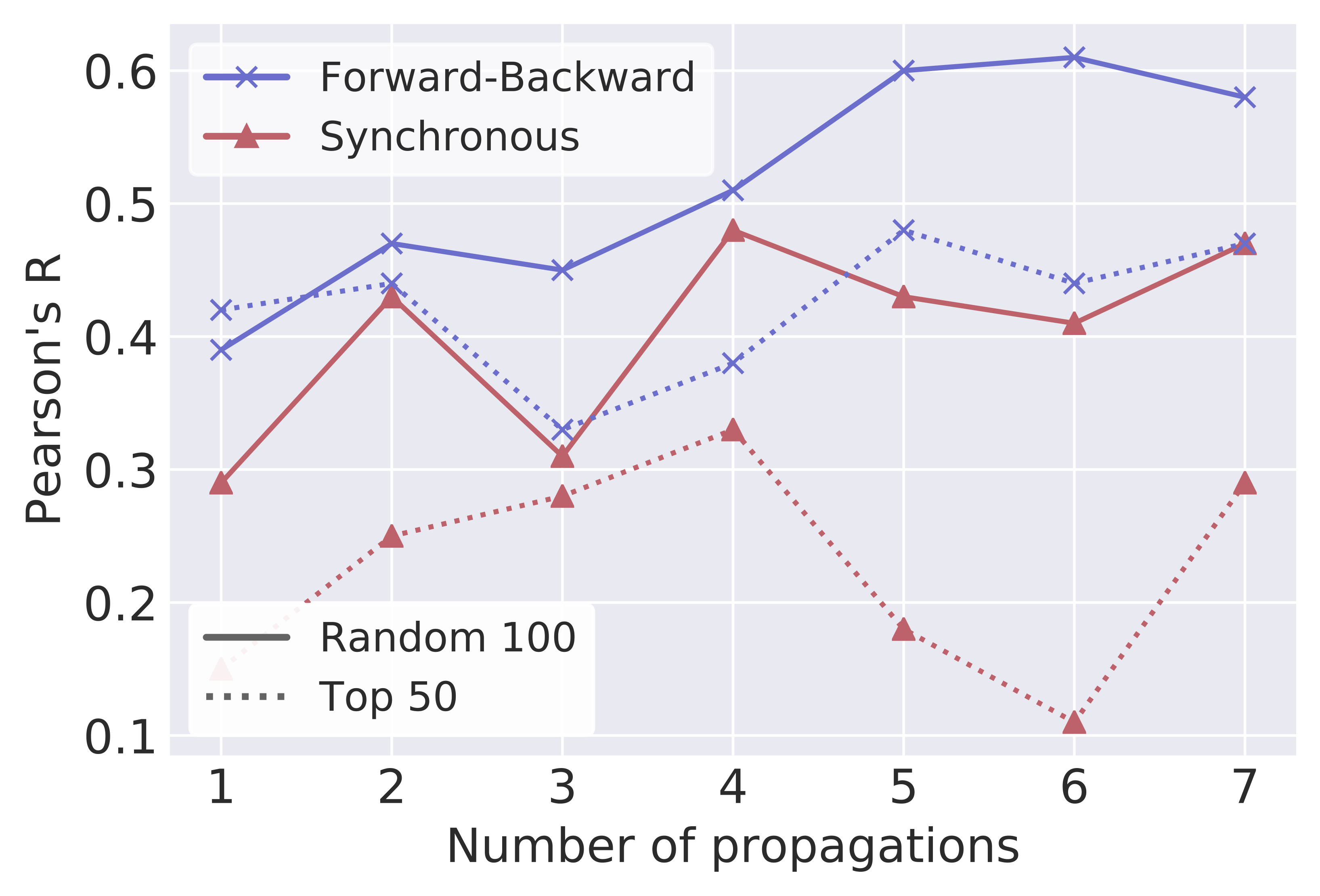
Number of propagation steps:
We now compare the forward-backward propagation scheme with the regular synchronous propagation scheme. Note that synchronous step corresponds to one full forward-backward phase. As shown in Figure 6, the forward-backward scheme consistently outperforms the synchronous scheme. More propagation steps also help improving the performance, with a diminishing return. While the forward-backward scheme is less amenable to acceleration from parallelization due to its sequential nature, it is possible to parallelize the evaluation phase across multiple GHNs when testing the fitness of candidate architectures.
| SP | PE | Correlation | |
|---|---|---|---|
| Random-100 | Top-50 | ||
| ✗ | ✗ | 0.24 | 0.15 |
| ✗ | ✓ | 0.44 | 0.37 |
| ✓ | ✓ | 0.68 | 0.48 |
Stacked GHN for architectural motifs:
We also evaluate different design choices of GHNs on representing architectural motifs. We compare 1) individual GHNs, each predicting one block independently, 2) a stacked GHN where individual GHN’s pass on their graph embedding without sharing parameters, 3) a stacked GHN with shared parameters (our proposed approach). As shown in Table 5, passing messages between GHN’s is crucial, and sharing parameters produces better performance.
6 Conclusion
In this work, we propose the Graph HyperNetwork (GHN), a composition of graph neural networks and hypernetworks that generates the weights of any architecture by operating directly on their computation graph representation. We demonstrate a strong correlation between the performance with the generated weights and the fully-trained weights. Using our GHN to form a surrogate search signal, we achieve competitive results on CIFAR-10 and ImageNet mobile with nearly 10 faster speed compared to other random search methods. Furthermore, we show that our proposed method can be extended to outperform the best human-designed architectures in setting of anytime prediction, greatly reducing the computation cost of real-time neural networks.
References
- Designing neural network architectures using reinforcement learning. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §2.
- Accelerating neural architecture search using performance prediction. In NIPS Workshop on Meta-Learning, Cited by: §2.
- Understanding and simplifying one-shot architecture search. In Proceedings of the 35th International Conference on Machine Learning (ICML), Cited by: §2, §2, Table 1.
- SMASH: one-shot model architecture search through hypernetworks. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Cited by: §1, §1, §1, §2, §2, §3, Table 1.
- Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Cited by: §3, §5.1.1.
- Peephole: predicting network performance before training. arXiv preprint arXiv:1712.03351. Cited by: §2.
- Improved regularization of convolutional neural networks with cutout. arXiv preprint arXiv:1708.04552. Cited by: §5.1.1.
- DPP-net: device-aware progressive search for pareto-optimal neural architectures. In European Conference on Computer Vision (ECCV), Cited by: §2.
- Multi-objective architecture search for cnns. arXiv preprint arXiv:1804.09081. Cited by: §2.
- SpeedBoost: anytime prediction with uniform near-optimality. In Proceedings of the 15th International Conference on Artificial Intelligence and Statistics (AISTATS), Cited by: §5.2.
- Hypernetworks. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §1, §2, §3.
- Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.3.
- Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.3.
- Long short-term memory. Neural Computation 9 (8), pp. 1735–1780. Cited by: §3.
- MONAS: multi-objective neural architecture search using reinforcement learning. arXiv preprint arXiv:1806.10332. Cited by: §2.
- Multi-scale dense networks for resource efficient image classification. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Cited by: §5.2, §5.2, §7.1, §7.3.
- Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §4.3.
- Adam: a method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), Cited by: §5.1.1.
- Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §3.
- Learning multiple layers of features from tiny images. Technical report University of Toronto. Cited by: §5.1.1, §5.
- Gated graph sequence neural networks. In Proceedings of the 4th International Conference on Learning Representations (ICLR), Cited by: §3, §4.4.
- Graph partition neural networks for semi-supervised classification. In ICLR Workshop, Cited by: §4.4.
- Progressive neural architecture search. In European Conference on Computer Vision (ECCV), Cited by: Table 3.
- Hierarchical representations for efficient architecture search. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Cited by: §2.
- DARTS: differentiable architecture search. arXiv preprint arXiv:1806.09055. Cited by: §2, §2, §5.1.1, Table 2, Table 3.
- Neural architecture optimization. arXiv preprint arXiv:1808.07233. Cited by: §2.
- Evolving deep neural networks. arXiv preprint arXiv:abs/1703.00548. Cited by: §2.
- Efficient neural architecture search via parameters sharing. In Proceedings of the 35th International Conference on Machine Learning (ICML), Cited by: §1, §2, §4.3, §5.1.1, §5.3, Table 2.
- Regularized evolution for image classifier architecture search. arXiv preprint arXiv:1802.01548. Cited by: §2, Table 3, §7.3, §7.3.
- Large-scale evolution of image classifiers. In Proceedings of the 34th International Conference on Machine Learning, Cited by: §2.
- Imagenet large scale visual recognition challenge. International Journal of Computer Vision 115 (3), pp. 211–252. Cited by: §5.1.2, §5.
- The graph neural network model. IEEE Trans. Neural Networks 20 (1), pp. 61–80. Cited by: §3.
- Learning to control fast-weight memories: an alternative to dynamic recurrent networks. Neural Computation 4 (1), pp. 131–139. Cited by: §2.
- A ‘self-referential’weight matrix. In International Conference on Artificial Neural Networks (ICANN), Cited by: §2.
- MnasNet: platform-aware neural architecture search for mobile. arXiv preprint arXiv:1807.11626. Cited by: §2.
- Backpropagation through time: what it does and how to do it. Proceedings of the IEEE 78 (10), pp. 1550–1560. Cited by: §3.
- Genetic CNN. In IEEE International Conference on Computer Vision (ICCV), Cited by: §2.
- Resource-efficient neural architect. arXiv preprint arXiv:1806.07912. Cited by: §2.
- Neural architecture search with reinforcement learning. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Cited by: §1, §2, §5.1.1.
- Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Cited by: §1, §2, §4.3, Table 2, Table 3, §7.3, §7.3.
7 Appendix
7.1 Search space
Standard image classification on CIFAR-10 and ImageNet
The search space for CIFAR-10 and ImageNet classification experiments includes the following operations:
-
identity
-
convolution
-
separable convolution
-
separable convolution
-
dilated separable convolution
-
dilated separable convolution
-
convolution followed convolution
-
max pooling
-
average pooling
A block forms an output by concatenating all leaf nodes in the graph. Blocks have 2 input nodes which ingest the output of block and block respectively. The input nodes are bottleneck layers, and can reduce the spatial size by using stride 2.
Anytime prediction on CIFAR-10
The search space for the CIFAR-10 anytime prediction experiments includes the following operations:
-
convolution
-
convolution
-
convolution
-
max pooling
-
average pooling
In the anytime setting, nodes concatenate their inputs rather than sum. Thus, the identity operator was removed as it would be redundant. The search space does not include separable convolutions so that it is comparable with our baselines (Huang et al., 2018). Block 1 contains nodes which may operate on any of the 3 scales (). Block 2 contains nodes which can only operate on scales and . Block 3 only contains nodes which operate on the scale . We fix the number of exit nodes. These choices are inspired by Huang et al. (2018)
7.2 Graph HyperNetwork details
Standard image classification on CIFAR-10 and ImageNet
While node embeddings are initialized to a one-hot vector representing computational operator of the node, we found it helpful to pass the sparse vector through a learned embedding matrix prior to graph propagation. The GHN is trained for 200 epochs with batch size 64 using the ADAM optimizer with an initial learning rate 1e-3 that is divided by 2 at epoch 100 and 150. A naive hypernet would have a separate output branch for each possible node type, and simply ignore branches that aren’t applicable to the specific node. In this manner, the number of parameters of the hypernetwork scale according to the number of possible node computations. In contrast, the number of parameters for a one-shot model scale according to the number of nodes in the graph. We further reduce number of parameters by obtaining smaller sized convolutions kernels through the slicing of larger sized kernels.
Anytime prediction
In the anytime prediction setting, two one-hot vectors representing the node’s scale and presence of an early exit classifier are additionally concatenated to the first initialized node embedding. We found it helpful to train the GHN with a random number of nodes per block, with maximum number of allowed nodes being the evaluation block size. Because nodes concatenate their inputs, a bottleneck layer is required. The hypernetwork can predict bottleneck parameters for a varying number of input nodes by generating weights based on edge activations rather than node activations. We form edge activations by concatenating the node activations of the parent and child. Edge weights generated this way can be concatenated, allowing the dimensionality of the predicted bottleneck weights the be proportional to the number of incoming edges.
7.3 Final architecture training details
Cifar-10
Following existing NAS methods (Zoph et al., 2018; Real et al., 2018), the final candidates are trained for 600 epochs using SGD with momentum 0.9, a single period cosine schedule with , and batch size 64. For regularization, we use scheduled drop-path with a final dropout probability of 0.4. We use an auxiliary head located at 2/3 of the network weighted by 0.5. We accelerate training by performing distributed training across 32 GPUs; the learning rate is multiplied by 32 with an initial linear warmup of 5 epochs.
ImageNet Mobile
For ImageNet mobile experiments, we use an image size of . Following existing NAS methods (Zoph et al., 2018; Real et al., 2018), the final candidates are trained for 250 epochs using SGD with momentum 0.9, initial learning rate 0.1 multiplied by 0.97 every epoch. We use an auxiliary head located at 2/3 of the network weighted by 0.5. We use the same regularization techniques, and similarly accelerate training in a distributed fashion.
Anytime
Following Huang et al. (2018), the final candidates are trained using SGD with momentum 0.9. We train the models for 300 epochs use an initial learning rate of 0.1, which is divided by 10 after 150 and 225 epochs using a batch size of 64. We accelerate training with distributed training in a similar fashion as the CIFAR-10 classification and ImageNet mobile experiments. The number of filters for the final architecture is chosen such that the number of FLOPS is comparable to existing baselines.
7.4 Visualization of Final architectures
7.4.1 CIFAR-10 and ImageNet Classification
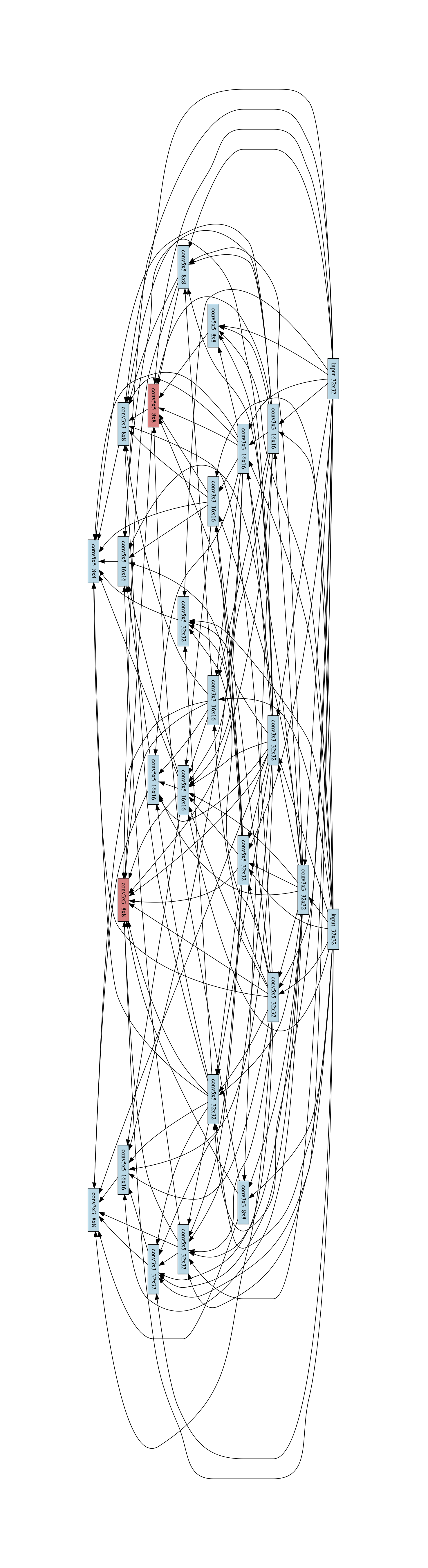
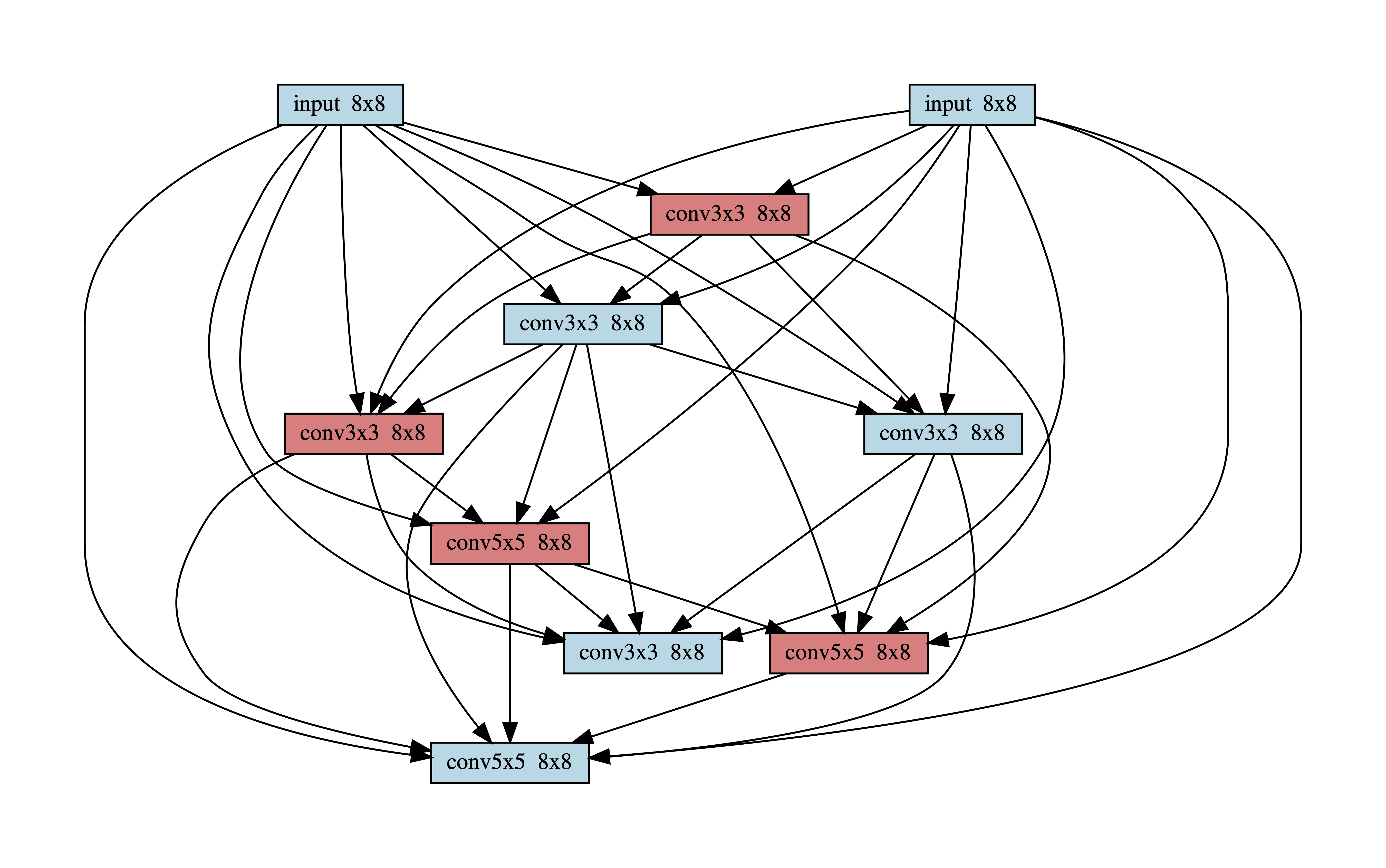
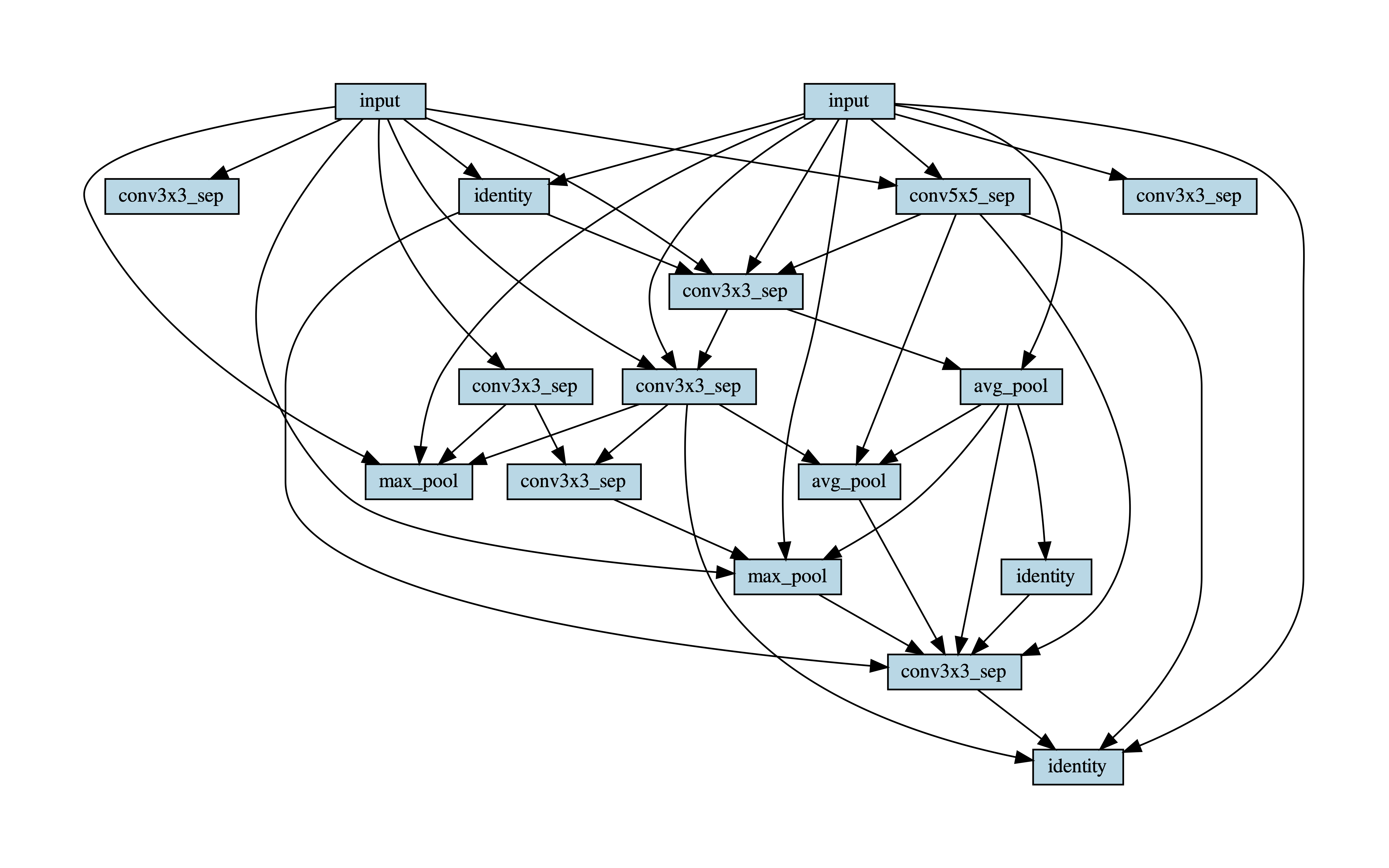
Figure 7 shows the best found block in the CIFAR-10 Experiments.
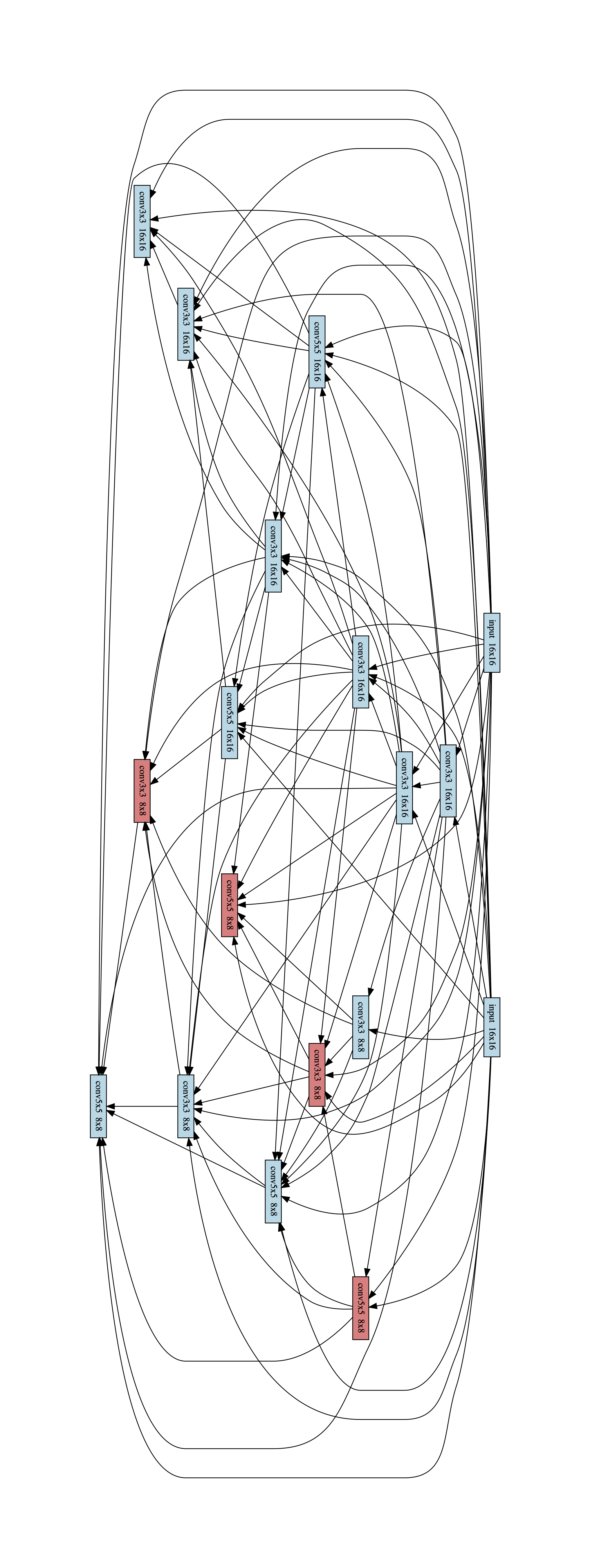
7.4.2 Anytime Prediction
Figures 8, 9 and 10 show blocks 1 2 and 3 of the best architecture found in the anytime experiments. The color red denotes that an early exit is attached to the output of the node.